云手机网页版 什么是数学领域的卷积运算

用于将两个函数或信号合并成一个新的函数或信号，以表示其中一个函数怎样去修改另一个函数的一种数学运算，是卷积操作，它在数学、信号处理、图像处理以及深度学习领域都存有广泛运用。于各种不同领域之中，卷积操作具体实现以及用途也许会存在差异，可是其基本数学原理却是相通的。

定义和数学表达

数学里，两个实数函数 f 与 g 的卷积这般定义，（f * g）(t) = ∫f(τ)g(t - τ)dτ ，这里 t 是变量，τ 是积分变量，此定义适用于连续函数情形kiayun手机版登录打开即玩v1011.玩看我最新关网.中国，而就离散函数或信号而言，卷积被定义成：（f * g） = Σfg ，这里 k 是求和索引，在这里能瞧见卷积体现出了一个函数在另一个函数之上的“滑动”效果，当中 g 意味着函数 g 相对于 f 的平移 。

直观理解

构想你拥有一个信号或者函数，像是一段乐曲或者一张图片，你期望借由某种途径去改变它，像是使图像模糊或者变换音乐的回声效果。卷积操作便是用来达成这种改变的工具。经由挑选适宜的卷积核（亦称作滤波器），你能够确定要怎样去修正原始信号或者图像。

图像处理中的应用

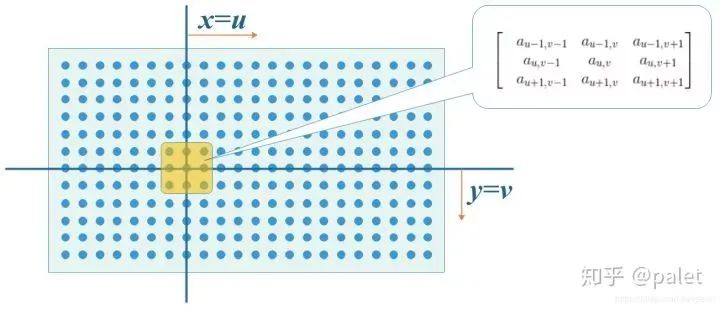
在图像处理这个范畴里，卷积运算常常被运用在图像滤波以及边缘检测等方面。比如说，有一个简单的平均滤波器，它能够借助与一个带有均匀权重的卷积核做卷积，以此达成图像的平滑处理，进而减少噪声。而边缘检测是经由识别像素强度的突变去达成的，所采用的卷积核会让这些快速变化的区域凸显出来。

深度学习中的应用

在深度学习里头，卷积神经网络，也就是 CNNs 啦，是那种专门设计出来处理有着类似网格结构数据的模型哟，比如说像图像呢，它能够被看成是像素所构成的二维网格哒。在 CNN 当中，卷积层会借助在输入数据之上滑动不一样的卷积核，然后开展卷积运算，以此来学习数据里面的特征呢。这种办法相当有效呀，究其原因在于它能够自动且高效地从数量众多的数据里学习特征，根本不需要手动去设计特征提取算法哒。

数学上的深入理解

其并非仅仅只是一种数学工具，它还可以用来体现数学中的许多深奥义理，比如，在信号处理里依照卷积定理，两个信号的卷积于傅立叶变换的情况下就等价于着这两个信号的傅立叶变换之逐点乘积，这一定理，它不单单在理论层面有着重要价值，而且还能为计算卷积提供一种更为高效的办法kiayun手机版登录，特别是在涉及大规模数据处理之际 。

卷积的变体

在实际运用当中，我们此外还能够碰到卷积的一些变化形式，像是交叉卷积以及相关性卷积。这些变化形式于某些特定的应用场景里面或许更为恰当适用。举例来说，在某些涉及图像处理的应用情形下，相关性卷积因为其具有直观的物理意义（就好比模板匹配）从而被予以广泛运用。

实例解析

假设我们在处理一维数字信号，我们有一个信号 f =

2, 3, 1, 0

与一个卷积核 g 等于 。依据离散卷积的定义，我们能够计算它们的卷积 f * g：

对函数f与函数g的乘积在0处的值进行计算时，其等式关系为，f与g的乘积在0处的值通过2乘以1加上3乘以0再加上1。
函数f与函数g相乘后在1处的值等于，3乘以1，加上，1乘以0，加上，0乘以负1，结果等于3 。
先算括号里的f与g相乘，再取其结果在自变量为2时的值，它等于1乘以1加上0乘以0。

通过卷积运算，将两个序列结合起来，进而生成一个新序列，这个简单例子对此予以展示。在图像处理里，若 f 是图像上的一个像素区域，同时 g 是一个边缘检测卷积核，那么这个操作能够助力我们识别图像中的边缘 。

总结

卷积操作，是一种强大且灵活的数学工具，它于众多领域kiayun手机版登录下载，均发挥着关键作用。明白卷积的基础概念，以及怎样去应用它，能够助力我们处理各类实际问题，从简易的信号处理，至繁杂的图像识别任务，再到深度学习模型的设计与实现。借助深入研读与探究卷积的特性，我们可以更优地领会这个强大工具的潜能，并知晓如何把它运用到我们所面临的特定问题里。