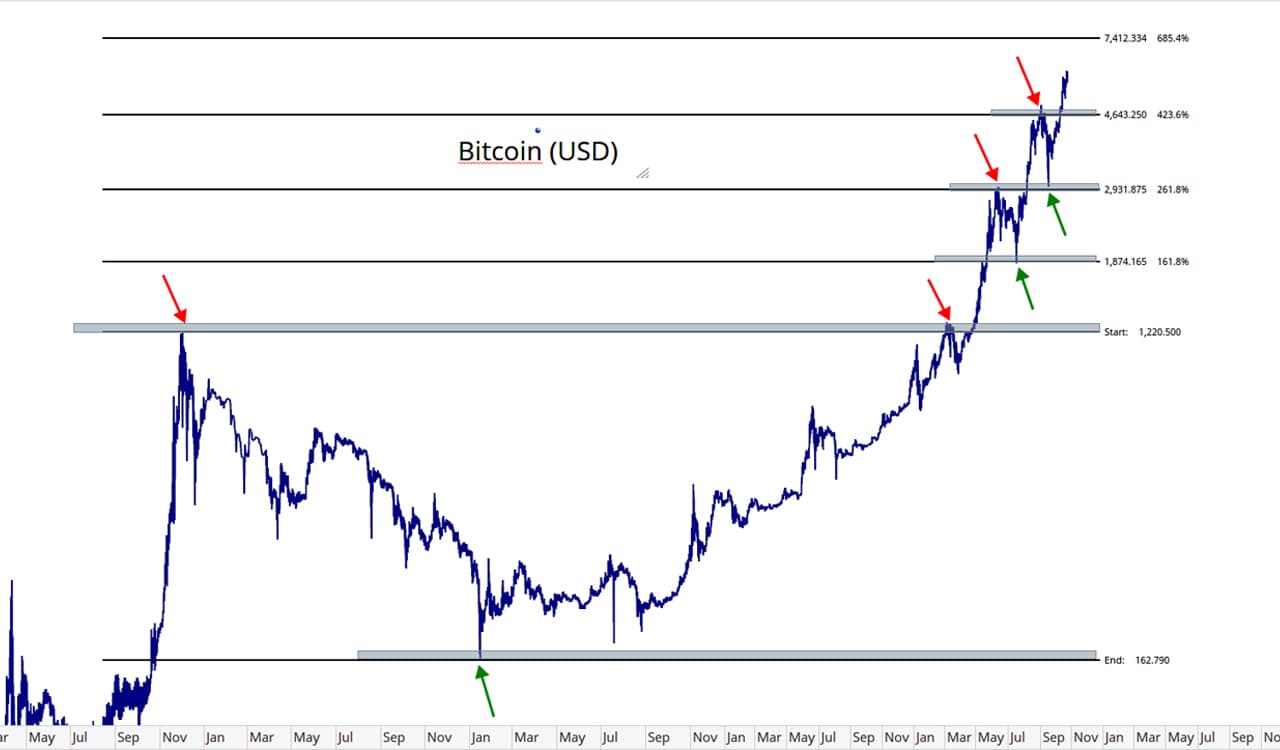
kiayun手机版登录app游戏登录入口.手机端安装.cc 为什么要使用卷积

怎么去解释卷积这个名词呢，“卷”到底是什么含义呢，以及“积”又有着怎样的意思呢 ？

卷积之中的“卷”，所指的乃是函数的翻转，即从g(t)转变为g(-t)的这一过程，与此同时，“卷”还存在着滑动的那种意味在其中，此乃吸取了网友李文清的建议。要是将卷积翻译为“褶积”，那么这个“褶”字便仅仅只有翻转的含义了。

卷积的“积”，指的是积分/加权求和。

在图像处理这个范畴里，卷积处理所产生的结果，实际上就是将每个像素周围的，哪怕是包含整个图像的像素都一一纳入考量，而之后针对于当前像素展开某种加权处理。如此一来，所谓的“积”是一种全局意义的概念，或者可以说是呈现出一种状如“混合”的情形，将两个函数于时间或者空间方面进行混合 。

实施“卷”（翻转）这一行为的目的实际上是施加一种约束，该约束规定了在“积”的时候所依据的参照是什么 。

在空间分析的场景，它指定了在哪个位置的周边进行累积处理。

2. 卷积背后的意义是什么，该如何解释？

图像处理

把一幅表示为f(x,y)的图像输入进去，经由经过特定设计而形成的卷积核g(x,y)来开展卷积处理，之后输出的图像便会出现模糊、边缘强化等各种各样的效果。

卷积的意义：

在图像处理中，卷积处理的结果，其实就是把每个像素周边的，甚至是整个图像的像素都考虑进来，对当前像素进行某种加权处理。所以说，“积”是全局概念，或者说是一种“混合”，把两个函数在时间或者空间上进行混合。

那为何要开展“卷”呢？开展“卷”（翻转）的意图实际上是施加一种约束，这种约束规定了在做“积”时以什么作为参照，在空间分析的情景里，它规定了在哪个位置的周边进行累积处理 。

针对图像的处理函数，像是进行平滑操作，又或是开展边缘提取工作，同样能够借助一个g矩阵予以呈现，情形如下：

注意，我们在处理平面空间的问题，已经是二维函数了，相当于：

那么函数f和g的在（u，v）处的卷积该如何计算呢？

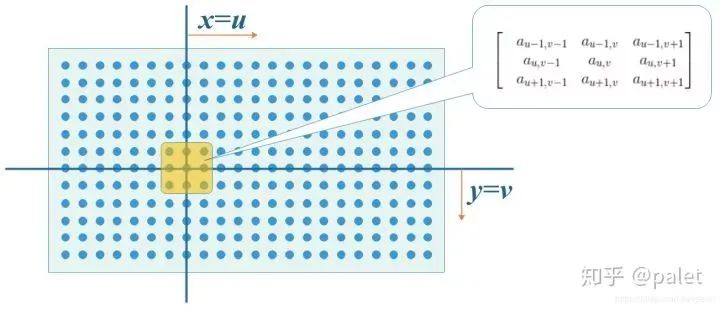
首先我们在原始图像矩阵中取出（u,v）处的矩阵：

接着要把图像处理矩阵进行翻转云手机网页版，这个翻转存在特别之处，并非沿着X轴以及Y轴这两个方向去翻转，而是顺着从右上到左下的对角线来翻转，这么做是本着为搭配后面的内积公式的目的，后续呈现如下：

可对比下图：

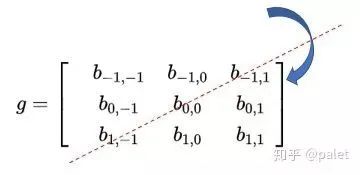
计算卷积时，就可以用和的内积：

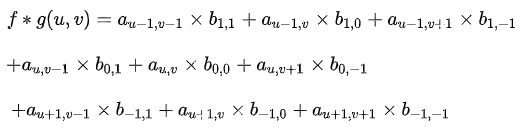
以上公式存在一个特性开·云体育app下载安装，进行乘法运算的两个相对应变量a、b的下标之和皆为（u、v），其意图在于针对这种加权求和予以一种限制。这亦是为何要把矩阵g予以翻转的缘由。以上矩阵下标之所以如此书写，且进行了翻转kia云手机版登录，是为了能让大家更明晰地瞧见跟卷积的关联。这般做的益处是利于推广，也利于领会其物理含义。实际于计算之际，均是采用翻转之后的矩阵，直接求取矩阵内积便可。

接下来对（u，v）处的卷积所作的计算，是沿着x轴或者y轴进行滑动，借此能够求得图像中不同位置的卷积，将其输出结果展现为处理以后图象（也就是经过了诸如平滑、边缘提取等一系列各种处理的图象） 。

倘若再进一步认真深入地去进行一些相对深邃的思考，随后当我们在着手计算图像卷积之际，我们把目光聚焦到原始图像矩阵之上，从中选取了处于（u,v）这个位置处的矩阵，但是这个选取行为背后有着怎样的缘由呢，为什么一定要去取这个具体位置的矩阵呢，实则从本质层面来讲，这是为了能够切实满足上述所提及的那些约束条件。这是因为，我们当下要去完成对（u，v）处的卷积计算工作，然而需要知晓的是，g矩阵是呈现为3x3样式的矩阵，当我们进一步去考量时，要使得下标与这个3x3矩阵进行相加之后的结果恰好是（u,v），那么在这个时候，唯一可行的办法就是去选取原始图像当中以（u，v）作为中心的那个3x3矩阵，也就是如同图中所展示的阴影区域那样呈现态势的矩阵。

将其推广开来，要是g矩阵并非3x3，而是6x6，那么我们就得在原始图像里选取以（u，v）作为中心的6x6矩阵来展开计算。由此能够明白，这种卷积是把原始图像里相邻的像素统统纳入考量，予以混合。相邻区域的范围由g矩阵的维度所决定，维度越大，涉及到的周边像素数量就越多。而矩阵的设计，决定了这种混合输出的图像与原始图像相比较，到底是变得模糊了，还是更加锐利了。

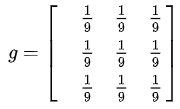
举个例子，像下面这样的图像处理矩阵，会致使图像变得更加平滑，看起来更模糊，这是由于它对周边像素开展了平均处理：

接下来，会有这样一个图像处理矩阵，它将会为像素值发生明显改变的区域带来更显著的变化，以此来强化边缘，与此同时，对于那些变化较为平缓的区域而言，它是不会产生任何影响的，最终借此达成提取边缘的目标，这般情况之下：