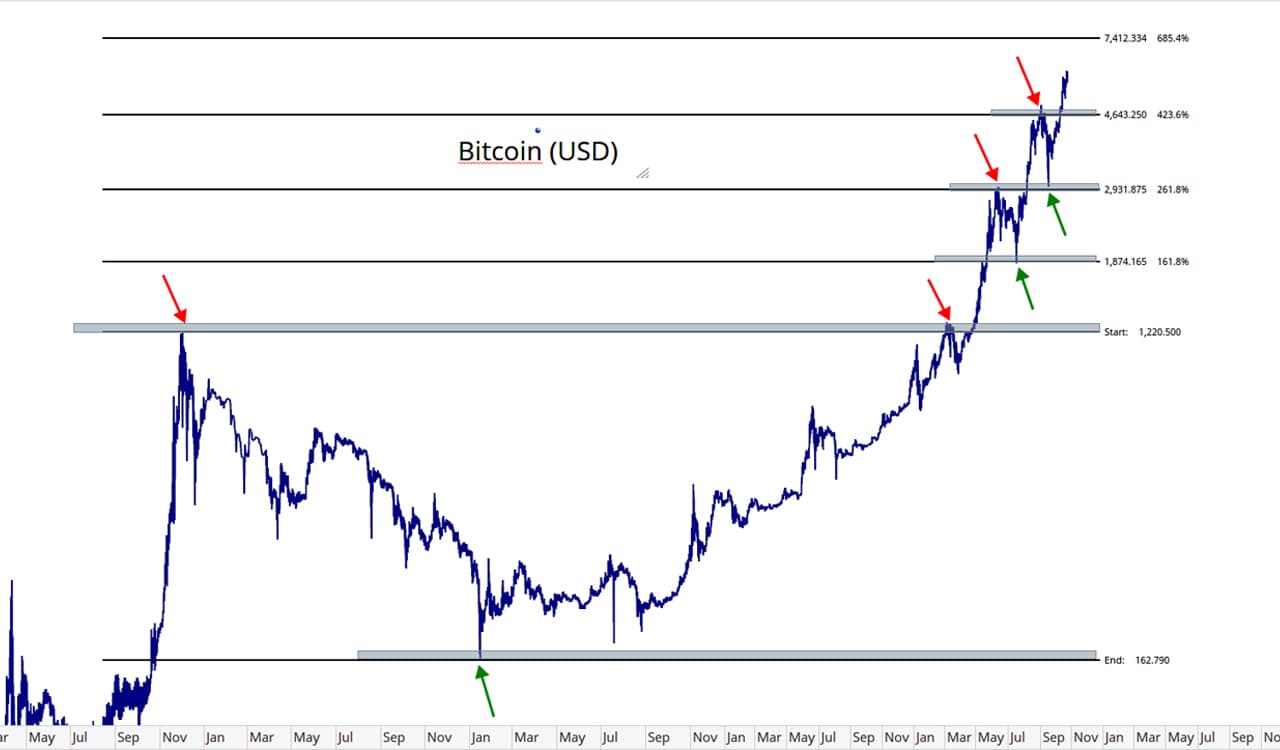
开·云app体育登录入口 浅谈菲波纳契数列的内涵和应用价值.doc

99 数学本四班的莫少勇，其指导教师是孙丽英。摘要方面，本文始于菲波那契数列kiayun手机版登录app游戏登录入口.手机端安装.cc，经由探究其数学内在含义以及它于实际生活里的运用，来增强学生对于数学的鉴赏能力，初步构建起数学建模的思想，如此一来提升运用数学知识剖析实际问题的能力。i 数列、黄金数、优选法，数学之美，不但存有形式上的和谐美妙，而且具备内容上的严谨美妙；不但拥有语言的简明、精巧美妙，而且具有公式、定理的结构整体美妙；不但存在逻辑、抽象美妙，而且有创造应用美妙。率先从数的比例里求取美的形式，发现黄金数的是古希腊的毕达哥拉斯学派，神奇的菲波纳契数列作为一项重大发现，是在黄金数之后出现的，它号称“黄金数列。i数列被提出时，和兔子的繁殖问题相关，它是一个极为重要的数学模型 。关于这个问题是这样的，存在一对小兔，在第二个月时它们成年，到第三个月生下一对小兔，之后每个月能生产一对小兔，所生的小兔在第二个月成年，第三个月又生产另一对小兔，往后每月都生产小兔一对，假设每产下一对小兔必定是一雌一雄，并且都没有死亡，那么试问一年之后总共会有小兔多少对呢？对于从\(1\)，\(2\)，一直到\(n\)，令\(Fn\)表示第\(n\)个月开始时兔子的总对数，将\(Bn\)、\(An\)分别确定为未成年和成年的兔子（也就是小兔和大兔）的对数，所以\(Fn = An + Bn\)。依据题设条件，有月份\(n\)为\(1\)、\(2\)、\(3\)、\(4\)、\(5\)、\(6\)等等时，\(An\)呈现\(1\)、\(1\)、\(2\)、\(3\)、\(5\)、\(8\)等等的情况，\(Bn\)呈现\(1\)、\(1\)、\(1\)、\(2\)、\(3\)、\(5\)等等的情况，\(Fn\)呈现\(1\)、\(1\)、\(2\)、\(3\)、\(5\)、\(8\)、\(13\)等等的情况。显然可以看出，\(F1 = 1\)，\(F2 = 1\)，而且从第三个月开始，每个月的兔子总数恰好等于它前面两个月的兔子总数之和，于是按照这样的规律我们得到一个带有初值的递推关系式：若我们规定\(F0 = 1\)，是以\(i\)数列的通常定义，也就是数列\(1\)，\(1\)，\(2\)，\(3\)，\(5\)，\(8\)，\(13\)，\(21\)，\(34\)，\(55\)，\(89\)等等，这串数列的特点是：其中任一个数都是前两数之和。这个关于兔子的问题，是由意大利数学家梁拿多（Leomardo），在其撰写的《算盘全集》里提出来的，梁拿多又被叫做菲波纳契（i），所以这个数列被称作菲波纳契数列，i数，它的通项是Fn= 。

()n+1-()n+1

由法国数学家比内（）求出的。（1）i数列通项的证明，我们实现它可以通过求解常系数线性齐次递推关系，或者利用生成函数法。证法一：因其菲波纳契数列有关于递推关系的情况，它是一个2阶的线性齐次递推关系，其递推方程为x2－x－1＝0，特征根有相应的值，所以，通解是那种形式Fn＝C1（）n＋C2（）n这样代入初值去确定C1、C2，能得到方程组，解这方程组得相应的那些结果，就是C1等于什么，C2等于什么等等具体的值，所以原递推关系的解是Fn等于什么之类 。 （表述中括号部分因原文缺失具体内容所以未很好替换，但尽力按要求表述，导致改写完也较混乱，主要因原文部分关键缺失影响准确改写）。

()n+1-()n+1

证法二：设 Fn 的生成函数是 F(x)，那么就有 F(x)=F0+F1x+F2x2+等等一直到 Fnxn+等等，x(F(x)-F0)=F1x2+F2x3+一直到 Fn - 1xn+等等，x2F(x)=F0x2+F1x3+等等kiayun手机版登录打开即玩v1011.玩看我最新关网.中国，把以上式子从两边由上而下进行作差，得到 F(x)(1 - x - x2)+x=F0+F1x+(F2 - F1 - F0)x2+(F3 - F2 - F1)x3+等等=1+x+0+0+等等，所以 F(x)=等于等于 +=+，由解得 A=，B=开·云体育app下载安装，所以 F(x)=-，所以取 x=1，k=n，那么 Fn= 。

()n+1-()n+1

(2)在i数列当中，。记载bn等于，那么就有b0等于等于1，b1等于等于，b2等于等于……，b3等于等于……，b4等于等于，b5等于等于……，bn等于。在求取数列的极限以前，我们首先要去证明以下的两个命题:(i)引理:i数列的任意相邻四项符合Fn减去2乘以Fn加上1减去Fn乘以Fn减去1等于负1的n次方，n大于等于3。证明:依据行列式与线性方程组的关系，方程组的解是x等于等于Fn减去1，y等于是……

()n+1-()n+1

等于Fn，所以Fn - 1、Fn符合原方程组，于是存在将以上方程组两边对应相乘的情况，得出等于，进行整理 。