kia云手机版登录 【CNN】很详细的讲解什么以及为什么是卷积（Convolution）！

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

1、对卷积的困惑

曾经在很早之前就学习过卷积这个概念，不过一直都没弄明白，教科书通常会给出定义，会给出众多性质，还会运用实例跟图形来进行解释，然而到底为何要如此设计，如此计算，其背后的意义是什么，常常说得不清楚；作为一个有学物理背景出身的人而言，要是一个公式给不出结合实际的直观通俗解释，也就是背后的“物理”意义，就会感觉缺了些什么，觉得不是真正弄明白了，。

通常情况下，教科书之中，对于函数f、g的卷积f*g(n)的这般定义是用以下方式给出的：

连续形式：

离散形式：

并且，还做出了解释，首先针对g函数实施翻转操作，这等同于在数轴之上，将g函数从右侧挪移并褶合至左侧区域之间，而这恰好就是卷积的“卷”这一概念的由来所在了。

接着将g函数朝着n进行平移，于这个特定位置把两个函数所对应的点相乘，随后相加，此过程即为卷积的“积”的过程 。

这仅仅是针对于计算方式角度而言，对公式展开了解释，就数学范畴来讲毫无破绽，然而进一步予以追问，为何要先行展开翻转之举，而后才作平移之动，这般的设计存有怎样的意图呢？依旧略微带着些费解的意味 。

在知乎，不少热心网友针对卷积给出诸多形象例子予以解释，像卷地毯、丢骰子、打耳光、存钱之类。读完后觉着极为生动有趣，然而仔细思索一番，却仍感觉某些地方仍旧未阐释清晰，甚至或许存在瑕疵，又或者能够加以改进（后续我会针对这些展开一些分析）。

怀着疑问思索了两个夜晚，最终感觉有些疑问被想透彻了，因而就将其撰写出来与网友予以分享，一同学习进步。不正确的地方欢迎给予评论批评指正。 。 。

明确一下，这篇文章主要想解释两个问题：

对于卷积这个名词该如何去进行解释呢，所谓的“卷”究竟意味着什么呢，而其中的“积”到底又有着怎样的含义呢？

2. 卷积背后的意义是什么，该如何解释？

2、考虑的应用场景

为了更好地理解这些问题，我们先给出两个典型的应用场景：

1. 信号分析

有一个以f(t)作为输入的信号，经过一个其特征能够用单位冲击响应函数g(t)来描述的线性系统之后，那输出信号会是什么呢？实际上借助卷积运算便能够得到输出信号。

2. 图像处理

将一幅图像f(x,y)输入进去，通过经过特定设计的卷积核g(x,y)来进行卷积处理，在处理之后，输出的图像就要会得到模糊、边缘强化等各种各样的效果。

3、对卷积的理解

对于卷积这个名词的认知是这样的，所说的两个函数相卷积，从本质上来说，就是先把其中一个函数进行翻转操作，之后再开展滑动叠加的行为 。

于连续情形时，叠加所指的便是针对两个函数的乘积去求取积分，在离散情形下那便是加权求和，鉴于此为了简单方便起见，于是就将其统一称作叠加 。

整体看来是这么个过程：

使其翻转，接着进行滑动，随后予以叠加，之后又进行滑动，再接着予以叠加，之后再次进行滑动，然后再进行叠加.....

多次滑动得到的一系列叠加值，构成了卷积函数。

卷积之中的“卷”，所指的乃是函数的翻转，即从g(t)转变为g(-t)的这一过程，与此同时，“卷”还存在着滑动的意味蕴含其中（此为吸取网友李文清的建议），要是将卷积翻译作“褶积”，则这个“褶”字就仅仅具备翻转的含义了 。

卷积的“积”，指的是积分/加权求和。

存在一些文章，仅仅着重于滑动叠加求和，却并未提及函数的翻转，我认为这样是不全面的，那部分篇章，对于“卷”的理解，实际上是“积”，我认定这属于张冠李戴。

对卷积的意义的理解：

从“积”的过程能瞧见，我们所获取的叠加值，属于全局的理念。拿信号分析来说，卷积的成果不但跟当下时刻输入信号的响应值存在关联，还跟过往所有时刻输入信号的响应均有关系，考量了对过去所有输入效果的累积。于图像处理里，卷积处理的结果，实际上就是将每个像素周边的，乃至整个图像的像素都纳入考量，针对当前像素开展某种加权处理。因此可以这么讲，“积”属于全局范畴内的概念，或者换句话来说，它是一种“融合”，是将两个函数于时间方面或者空间层面展开融合 。

2. 那么为何要开展“卷”呢？直接做乘法难道不行吗？依我之理解，开展“卷”（翻转）的意图实际上是施加一种限定，它明确了在做“积”的时候依据什么来参照。在信号分析的情形下，它明确了在哪个特定的时间点的前后去开展“积”。在空间分析的情景里，它明确了在哪个位置的周边进行累积处置。

4、举例说明

下面举几个例子说明为什么要翻转，以及叠加求和的意义。

例1：信号分析

如图所示，输入信号为f(t)，其是随时间变化的，系统响应函数是g(t)，图中的响应函数随时间呈指数下降，其物理意义表明，若在t = 0时刻存在一个输入，那么随着时间推移，该输入会持续衰减，也就是说，到了t = T时刻，原本在t = 0时刻的输入f(0)的值会衰减成f(0)g(T) 。

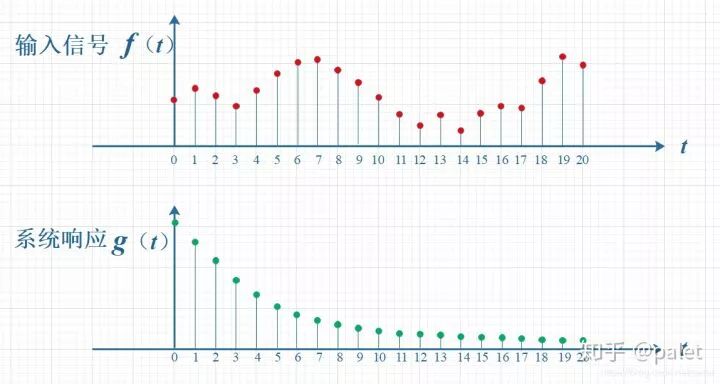
鉴于信号是以连续的方式输入的，这意味着，在每一个时刻都会有新的信号进入，所以，最后的输出呈现的是所有先前输入信号所产生的累积效果。如下方图示所展现的那样，在T等于10这个时刻，输出的结果与图里带有标记的区域整体存在关联。其中，f(10)由于是刚刚输入的，所以它的输出结果应当是f(10)g(0)kia云手机版登录，而时刻t为9时输入的f(9)，仅仅经历了1个时间单位的衰减，所以产生的输出理应是f(9)m(1)，依此类推，也就是图中虚线所描绘的那种关系。将这些对应点进行相乘操作，之后再对其进行累加，所得到的结果乃是T等于10时刻的输出信号数值，而且这个结果同样是f与g这两个函数于T等于10时刻的卷积数值。

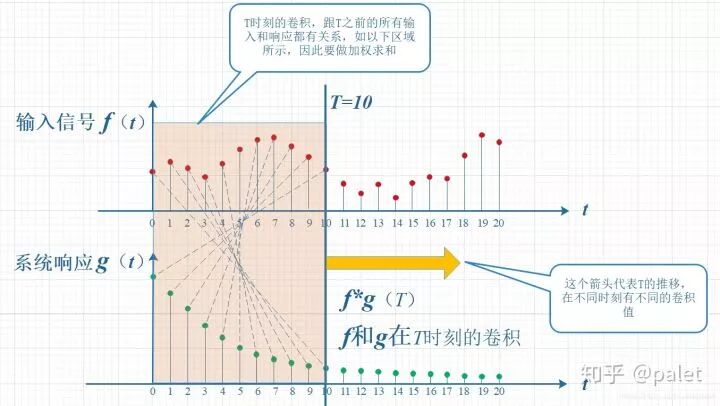
显然，上面那种对应关系，看上去相对比较难看，并且是拧着呈现的，所以，我们将g函数进行对折操作，使其变为了g(-t)，如此一来，看上去可就略显得好看一些了。瞧见了没？这便是为何卷积中会有“卷”，会存在翻转这种情况的缘由，这是依据其物理意义而得出的 。

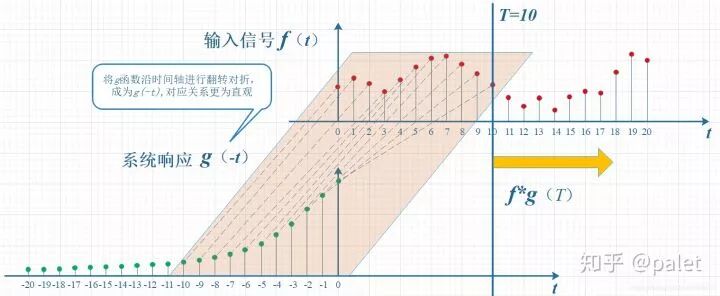
上面的图，尽管看上去没有拧着，已然顺过来了，可是看起来仍存在些许错位，因而再往更进一层平移T个单位，如此便成了下面的图。它就是在本文起始给出的卷积定义的一种关于图形的表述：

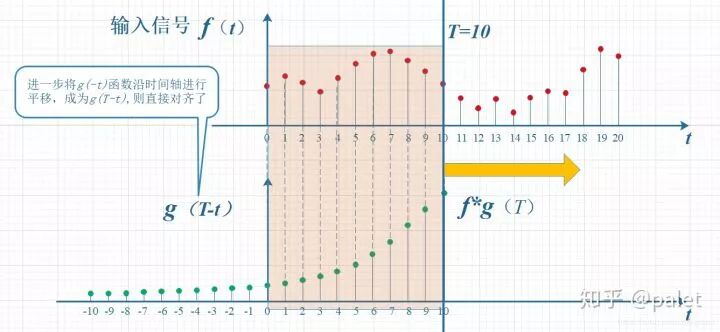
所以，于上述计算T时刻的卷积之际，需维持的约束便是：t加上（T减去t）等于T 。此种约束的意义，大家能够自行去体会 。

例2：丢骰子

关于本问题，也就是那个如何通俗易懂地 去解释掉卷积的问题里，排名处于首位的马同学所提到一个很好例子，下文中的一些图是 源自于马同学的文章摘取到此这儿得表示心怀深深谢意，其运用丢骰子这种方式 对卷积的应用作出了说明 。

现存在一个需要去解决的问题，此问题内容为，存在两枚骰子，这两枚骰子都进行抛投的动作，在抛投之后，需要知晓这两枚骰子各自所呈现的点数相加之和为4的概率究竟是多少 ？

细究起来，存在着这样的状况，即两枚骰子所呈现的点数加起来成为4的情形有三种，分别是，一种是1加上3其结果等于4，还有一种是2加上2其结果等于4，另外一种是3加上1其结果等于4 。

因此，两枚骰子点数加起来为4的概率为：

写成卷积的方式就是：

在这里我想进一步用上面的翻转滑动叠加的逻辑进行解释。

首先，鉴于两个骰子出现的点数之和为4，为了达成这个限制性条件，我们依旧将函数g进行翻转操作，接着把阴影区域上下所对应的数字进行相乘运算，随后进行累加，这等同于求取自变量为4时的卷积值，情况如下列图形所展示的那样：

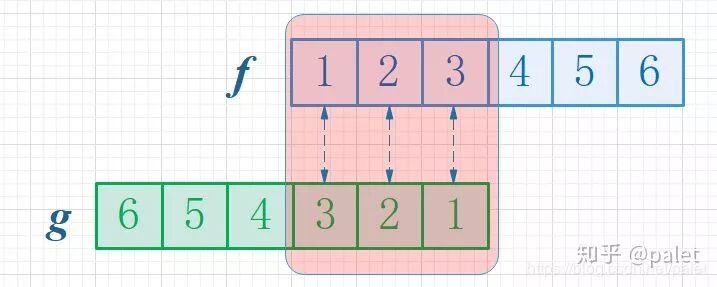
进而，这般翻转过后，能够便利地予以推广用以求取两个骰子点数之和为n时的概率，此概率为f与g的卷积f*g(n)，如同下面这幅图所展示的那样：

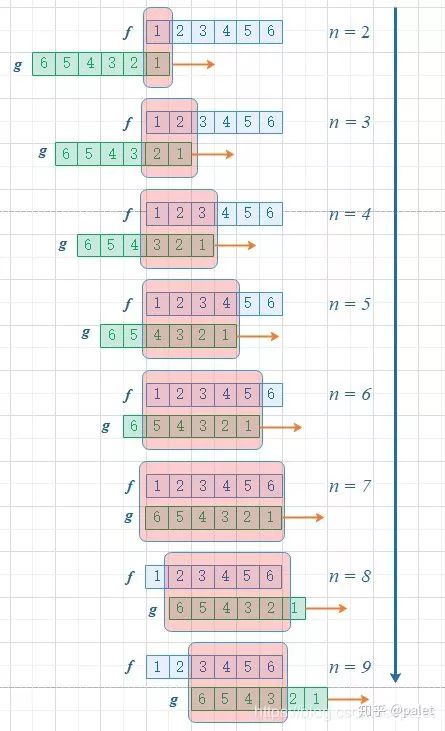
从上面的图能够看到，函数g的滑动，会致使点数和增大。在此例子里，对于f和g的约束条件是点数和，它同样是卷积函数的自变量。要是有兴趣，还能够算一算，倘若骰子每个点数出现的概率是_equal几率_一样的，那么当两个骰子的点数和n等于7的时候，概率是最大的。

例3：图像处理

引用知乎问题 如何通俗易懂地解释卷积？里中马同学的例子，图像也能够被表示成矩阵形式，（下图是从马同学的文章里摘取的） 。

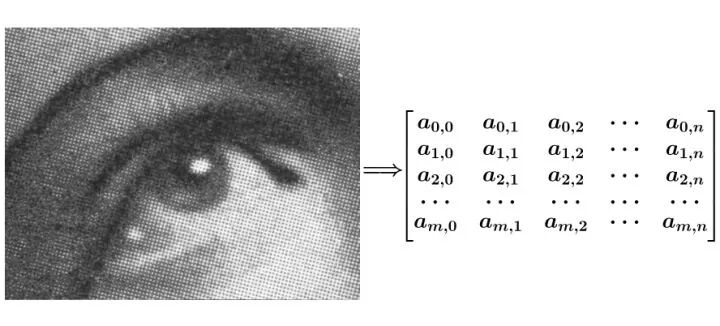
用于对图像进行处理的函数，像平滑这种开·云app体育登录入口，或者是边缘提取这类，同样能够借助一个g矩阵予以表示，情况如下：

注意，我们在处理平面空间的问题，已经是二维函数了，相当于：

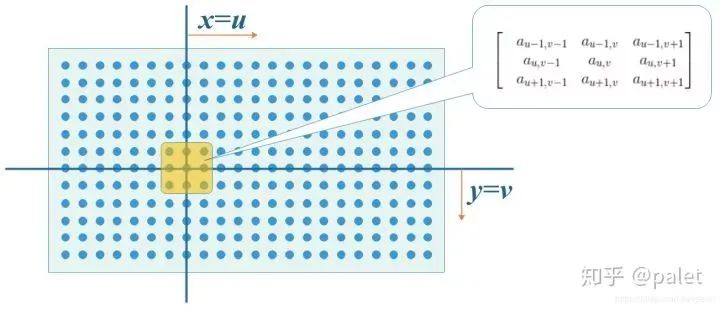
那么函数f和g的在（u，v）处的卷积该如何计算呢？

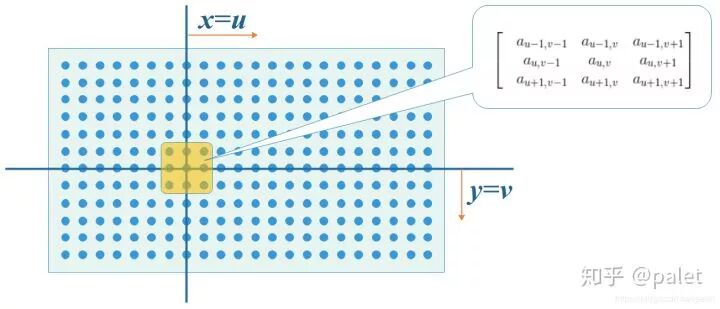
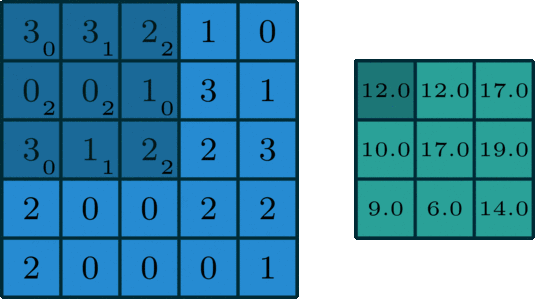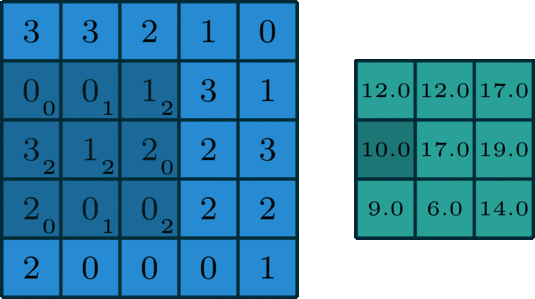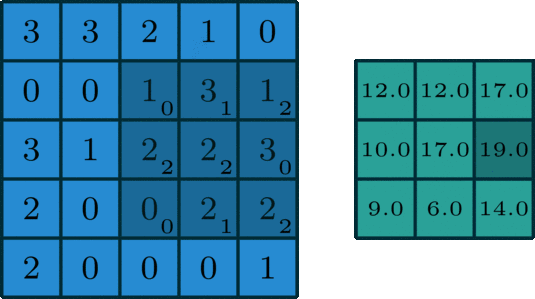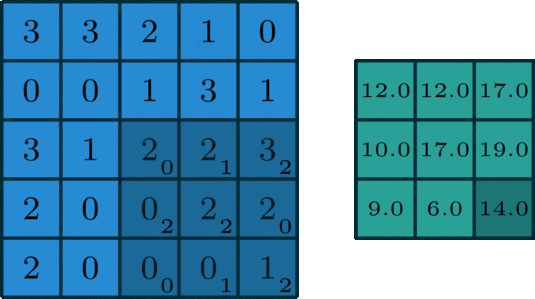
首先我们在原始图像矩阵中取出（u,v）处的矩阵：

然后呀，要对图像处理矩阵进行翻转，这个翻转呢有那么点意思，它可不是沿着x轴和y轴这两个方向去翻转的哦，而是沿着从右上到左下的对角线来翻转，这么做是为了去凑后面的内积公式，情况如下：

可对比下图：

计算卷积时，就可以用和的内积：

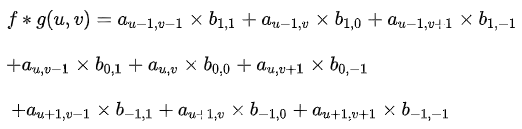
请注意，以上公式存在一个特点，做乘法时，两个对应变量a与b的下标之和俱为（u，v），其目的在于对这种加权求和予以一种约束。 这便是要将矩阵g进行翻转的缘由。 以上矩阵下标这般书写，且进行了翻转，是为了能让大家更清晰地瞧见跟卷积的关系。 如此做的好处乃便于推广，亦便于领会其物理意义。 实际于计算之际，皆使用翻转之后的矩阵，直接求取矩阵内积便可。

以上所进行的计算，计算的对象是（u,v）处的卷积，通过延x轴滑动，或者延y轴滑动，进而能够求出图像里各个位置的卷积，而其输出的结果是经过处理以后的图像，也就是那种经过了平滑处理、边缘提取等各种各样处理的图像。

那么，再进一步深入地进行思考，当我们在计算图像卷积的时候，我们所做的是直接于原始图像矩阵当中选取位于（u，v）处的矩阵，可是，为什么要选取这个特定位置的矩阵呢？从本质上来说，实际上是为了能够满足上述所提及的约束条件。原因在于，我们需要计算（u，v）处的卷积，并且，g矩阵是一个3x3的矩阵，要使得下标与这个3x3矩阵的和为（u，v），那么，唯一的方式就只能是选取原始图像里以（u，v）作为中心的这个3x3矩阵，也就是图中阴影区域所对应的矩阵。

顺着这个思路进一步拓展来说，如果g矩阵并非3x3，而是6x6的话，那我们便需要在原始图像里选取以（u，v）作为中心的6x6矩阵来展开计算。像这样可以看出，这种卷积实际上就是将原始图像当中相邻的像素全部考虑进去，进而进行混合操作。相邻的区域范围是由g矩阵的维度所决定的，维度越是大，所涉及到的周边像素也就会越多。而矩阵的设计，决定了这种经过混合输出的图像与原始图像相比较而言，到底是变得模糊了kiayun手机版登录入口，还是变得更加锐利了。

比如说，有这样一个图像处理矩阵，它会让图像变得更加平滑，且看起来更加模糊，原因在于它对周边像素做了平均处理 。

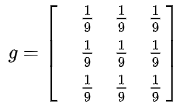
就是这样的图像处理矩阵，它会让像素值变化显著的区域变得更加突出，以此来强化边缘，并且在像素值变化平缓的地方产生不了影响，最终达成提取边缘的目标 。

5、对一些解释的不同意见

上述一些针对于卷积的形象化阐释，像是在知乎问题卷积为什么叫「卷」积？里荆哲所提出的，以及在知乎问题如何通俗易懂地解释卷积？内马同学等诸位所给出的这般比喻：

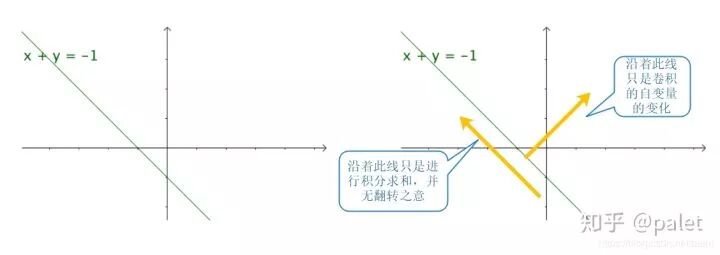
其实呀，图里面“卷”的那个方向呢，是顺着该方向给进行积分求和的方向哦，并没有那种翻转的意思哒。所以呀，这般解释呢，并没有将卷积的含义完整地描述出来哟，对于“卷”的理解是值得去进行商榷的呢。

6、一些参考资料

《数字信号处理（第二版）》程乾生，北京大学出版社

《信号与系统引论》 郑君里，应启珩，杨为理，高等教育出版社

好消息！
小白学视觉知识星球
开始面向外开放啦



下载1：OpenCV-Contrib扩展模块中文版教程
在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖模块扩展安装，SFM算法，立体视觉呈现，目标跟踪行为，生物视觉现象，超分辨率处理操作。等二十多章内容。

下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括把图像进行分割，对口罩展开检测，给车道线做检测，为车辆开展计数，给添加眼线这项操作，对车牌展开识别，对字符予以识别，对情绪进行检测，开展文本内容提取工作，对面部进行识别 。等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），将下面微讯号扫描一下加入群，记着写出： ”昵称 加上空格 学校或者公司 加上空格 研究方向“，像这样：”张三 空格 上海交大 空格 视觉 Slam“ 。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~