中考最易忽视的考点-数学在生活中应用

新课标的一个核心教学宗旨在于，借助数学原理处理现实层面的具体事务，这既是学生掌握知识、锻炼技巧并提升综合素养的体现开yun体育app官网网页登录入口，同时也是他们已经形成构造模型思维能力的证明。

构建数学模型解决实际问题基本步骤如下：

1、阅读、审题：

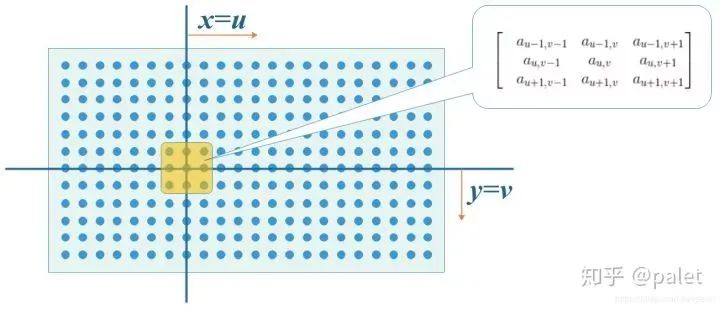
需要精简疑问，去除非核心内容，把握关键表述；为方便信息整理，宜借助图表（或图像）整理数据，利于发现数值关联。

2、建模、建立数学关系式：

将问题简单化、符号化，尽量借鉴标准形式，建立数学关系式。

3、运用数学知识

4、解释并回答实际问题

为了更加形象表示kaiyun全站app登录入口，我们可以参考下面的图标：

那么一起来看看数学和生活实际问题在中考中是怎么体现：

一、方程模型的应用

解题的基础环节包括：首先确立未知数，其次构建数学表达式，最后求解该表达式。处理实际问题时，核心要点在于：必须准确识别问题里的平衡条件，特别是要善于从文字描述中分析出这些平衡条件。分析平衡条件的过程，本质上就是将具体情境转化为数学框架的必要环节。

下面以2014年益阳的第18题为例：

二、方程不等式模型的综合应用

针对需要找到答案的问题，能够借助数学公式确定若干个变量之间的相互联系，然后经过替换和简化步骤，最终可以求得不等式条件下的整数值，由此可以形成多种可行的选择。

下面以2014年贵州黔东南州第23题为例：

某超市打算买入若干甲类与乙类玩具，明确五件甲类玩具的购入成本同三件乙类玩具的购入成本合计为231元，并且两件甲类玩具的购入成本同三件乙类玩具的购入成本合计为141元。

（1）求每件甲种、乙种玩具的进价分别是多少元？

当购买甲种玩具数量大于20件时，超出部分按七折计价，不足20件则按原价计算，设购买数量为x件，总金额为y元开元棋官方正版下载，求y与x的数学表达式。

在第二种情况里，超市需要从甲类和乙类玩具里选择一个种类购买，购买数量要超过二十件，请协助超市分析选择哪种玩具更节省开支。

三、函数模型在最值问题中的应用

求最值时，若题目未指定自变量，需先判断哪个量导致另一量改变，可把这两量分别当作自变量和因变量，构建函数表达式，并关注自变量的取值限制，如果是关于一次函数的最值情形，必须明确自变量的取值范围，再依据一次函数的单调性求解最值；如果是关于二次函数的最值情形，需通过配方法得到顶点，检查顶点横坐标是否属于自变量允许的区间，若不属于，应结合函数图像分析求解。

下面以2014年江苏徐州的第26题为例：

四、几何模型的应用

建立几何图形就是将现实问题里的核心内容转化为几何形态，比如线段、直角三角形，等腰三角形，平行四边形，梯形等，然后借助这些几何形态的特性来处理实际情形。

下面以2014年浙江宁波的第26题为例：

------------------------

想在考试中出类拔萃、脱颖而出吗？