云手机网页版 卷积的本质、物理意义及其在具体学科中的应用

卷积的诞生实际上就是冲着冲击函数来的，“冲击函数”是狄拉克所提出的符号，其目的在于解决那些具有瞬间作用特性的物理现象，古人讲过“说一堆大道理不如举一个好例子”，冲量这种物理现象能够很好地阐释“冲击函数”：在 t 时间之内针对一个物体施加 F 的力kiayun手机版登录打开即玩v1011.速装上线体验.中国，要是作用时间 t 非常小，作用力 F 特别大，然而要让 Ft 的乘积保持不变，也就是冲量维持恒定 。那么在以t作为横坐标的条件下，以及按F作纵坐标的坐标系当中，呈现出恰似一个面积恒定不变长方形的样式，其底边被挤压得窄窄的，而高度又被挤压得高高的，在数学范畴里它能够被挤压至无限高，即便它无限瘦、无限高，然而它依旧维持面积不变，即它没有被挤没，为了证实它的存在，可以针对它开展积分，积分就是求取面积，于是“卷积”这个数学怪物就这样诞生了。

卷积是“信号与系统”中论述系统对输入信号的响应而提出的。

意义

信号处理涉及把一个信号自一个信号空间映射至另一个信号空间，一般而言是从时域到频域，这其中还包括z域以及s域，信号所具备的能量等同于函数的范数这个概念，信号与函数是等同的，大家众所周知有个Paserval定理，这定理表明对于一种映射而言前后范数是保持不变的，在数学领域里这种映射被称作是保范映射，实际上在信号处理范畴中的变换基本上全部都是保范映射，只要Paserval定理能够成立那么就是保范映射，也就是能量不会发生改变的那种映射。

信号处理里是怎样产生卷积的呢。假定B是一个系统，在t时刻它的输入是x(t)，其输出是y(t)，该系统的响应函数是h(t)，按道理来讲，输出跟输入的关系应该是：

然而，实际情形是，系统输出同系统于 t 时刻的响应相关，且和其在 t 时刻之前的响应相关。不过系统存在衰减过程，因而t1(1)，此过程或许是离散的，也可能是连续的，所以 t 时刻的输出应当是，t 时刻之前系统响应函数于各时刻响应的叠加，这便是卷积，用数学公式表达即为

离散情况下就是级数了。

计算

卷积属于一种积分运算，这种运算能够用来描述线性时不变系统输入与输出间的关系，也就是说输出能够借助输入以及一个体现系统特性的函数（冲激响应函数）经卷积运算而获得。

一维卷积

首先，将函数x(k)针对原点进行反折操作，接着把反折后的函数向右移动t的距离，之后进行两个函数的相乘运算，再对相乘的结果进行积分操作，如此便得出了于t处的输出，针对每一个t的值就按照这种上头所讲的过程进行重复，最终就得到了输出曲线句号。

二维卷积

g(u,v)先绕其原点进行180度旋转，接着平移其原点，在u轴上向上平移x，在v轴上向上平移y，之后将两个函数相乘进行积分，从而得到一个点处的输出。

笑话—谈卷积的物理意义

有个担任七品官职的县令，喜好运用打板子这种方式去惩戒那些身处市井的无赖之人，并且存在着一个惯例，那就是倘若没有犯下重大罪行，仅仅打一板而已，之后便释放其回家，以此来显示自己如同爱护子女般对待百姓。

有个无赖，想要有出头之日却没什么希望，心道既然没法传播好名声，那传出坏名声也行。如何传出坏名声呢？靠炒作呀！怎样炒作呢？找名人呀！他自然而然就想到了他的行政长官，也就是县令 。

无赖于光天化日时节，伫立在县衙门前施行了撒尿之举，其后果是尽人皆可想象得出的，理所当然被邀入大堂遭受了板子责打，而后他昂首挺胸返回家中，卧床休养了一日，嘿呀！其身上未出现任何状况！次日他依样行事，全然漠视行政长官的仁慈以及衙门的体面，第三天、第四天……每日前往县衙门领受一个板子归来，还呈现出喜气洋洋之态，持续达一个月之久！这无赖的声名已然如同衙门口散发的臭气那般，传播至四面八方了！

县令大人皱起鼻腔，木然地瞅着案子上面的惊堂木，蹙着眉头思索一个疑问：这三十个大板子为何没能发挥效用呢？......遥想当初，本老爷在科举中榜上有名之时，数学可是拿到了满分成绩，今日怎么着也要把这个问题给解决掉：

人（系统）挨板子（脉冲）以后，会有什么表现（输出）？

费话，疼呗！

我问的是：会有什么表现？

瞧疼到何种程度，这般无赖模样的体格，每日承受一个板子，不会有任何事情发生，连哼一声都绝无可能，你也目睹了他那副得意洋洋的嘴脸，（输出0）。一次若连着揍他十个板子，他或许会皱皱眉头，咬咬牙，硬挺着不哼，输出1；揍到二十个板子，他会因疼脸部扭曲，像猪一样哼哼，输出3；揍到三十个板子，他可能会像驴一样嚎叫，一把鼻涕一把泪求你饶他一命，输出5；揍到四十个板子，他会大小便失禁，勉强哼出声来，输出1；揍到五十个板子，他连哼一下都没可能，输出0，死啦！

县令把坐标纸展开，将打板子的数量当作X轴，把哼哼的程度（输出）作为Y轴，画出了一条曲线：

呜呼呀！这曲线好似一座高山 ，弄不明白这个事儿 。为啥那个无赖连续挨了三十天平板 ，却不呼喊求饶呀 ？

呵呵，你进行一次击打所间隔的时长（Δτ为24小时）实在是太过漫长，因而那个无赖所承受的痛苦程度每天都处于一种利落的状态，不存在叠加情形，始终保持为一个恒定的数值；要是将击打板子的时间间隔予以缩短（建议Δτ为0.5秒），那么他的痛苦程度便会快速地叠加起来；待到这个无赖遭受三十个大板（t等于30）之时，痛苦程度抵达了其能够喊叫的极限，将会收获最佳的惩戒成效，再多进行击打就无法彰显出您的仁慈了。

还是不太明白，时间间隔小，为什么痛苦程度会叠加呢？

这和人有着关联，人针对于板子，板子存在所谓脉冲、输入、激励，人的这种情况与之响应密不可分。那么什么是响应呢？人遭受一个板子之后，疼痛的感觉便会在一天内渐渐消失，这里的一天是假设的，而且基于不同的人之上，疼痛感觉不会突然就没了，而是慢慢消失也就是衰减。如此这般，只要打板子的时间间隔十分小，每一个板子所引发的疼痛都无法及时完全衰减，每个板子引发的疼痛对于最终的痛苦程度都会有着不一样的贡献：

t个大板子所造成的痛苦程度，等于，第τ个大板子引起的痛苦，乘以，衰减系数，这些乘积的总和，句号

衰减系数是(t-τ)的函数，仔细品味。数学表达为：

提拿人的痛苦去讲卷积这样的事，实在太过残忍啦。除开人力以外，别的事物 是否也契合这么条规律呢 ？

呵呵，那县令大人终究是仁慈的。实际上呢，除了人之外呀，好多事情也是 adherence to this principle 的。仔细去思索一番，铁丝为何弯曲一回不会折断，迅速地弯曲好多回却会很容易就折掉呢 ？

嗯，一时间还没办法弄清楚，让本官缓缓地去思索——可是有一点是清清楚楚的——来人呐，把那个正在撒尿的无赖给抓取过来，狠狠地责打40大板！

可以这样去理解，T(τ)指的是第τ个板子，H(t - τ)表示的是第τ个板子所引发的痛苦到t时刻的痛苦程度，将所有的板子加起来得到的就是∫T(τ)H(t - τ)

卷积在具体学科中的应用

图像处理

用一个模板去和一幅图像展开卷积，针对图像上面的一个点，要让模板的原点跟该点相重合，接着模板上的点与图像上对应的点做相乘，随后各个点的积进行相加，如此便得到了该点的卷积值，对图像上的每个点都依照这样的方式来处理，因为大多数模板是对称的情况，所以模板不进行旋转，卷积属于一种积分运算，其作用是用来求取两个曲线重叠区域的面积，它能够被看作是加权求和，可用来消除噪声、实现特征增强。

把一个点的像素值用它周围的点的像素值的加权平均代替。

滤波中常用的图像处mask运算可视为常见于图像处理中的卷积，卷积属于线性运算，其广泛应用于图像滤波，卷积在数据处理里通过平滑达成既定成果，它具备平滑效应和展宽效应，进而起到所需作用。

电路学

卷积法把根据线性定常电路性质（像齐次性、叠加性、时不变性、积分性等），借助电路单位冲激响应h(t)来求解系统响应当作工具，系统激励通常能表示成冲击函数与激励函数的卷积，卷积属于高等数学里的积分概念，此概念中冲击函数幅度由每个矩形微元面积确定。

某种最为关键的卷积关系情形，乃是于信号跟线性系统或者数字信号处理里的卷积定理。借助此定理，能够把时间域或者空间域之中的卷积运算，等效成频率域的相乘运算，进而凭借FFT等快速算法，达成有效的计算，节约运算代价。

信号处理

求和（积分）是卷积，对于线性时不变系统，输入能分解成诸多强度各异的冲激之和的形式（在时域为积分），输出便是这些冲激分别作用于系统所产生响应的和（或积分），故而卷积的物理意义是体现了时域里输入、系统冲激响应以及输出间的关系。

系统冲击函数是在符合叠加原理的系统中才有的概念，卷积代表线性系统对输入信号的响应方式，其输出等于系统冲击函数和信号输入的卷积，使卷积成为系统对输入在数学上运算的必然形式，冲击函数实际上是该问题的格林函数解，点激励源作为强加激励求解某个线性问题的解，得到的格林函数即是系统冲击响应，所以在线性系统中系统冲击响应与卷积存在必然联系，信号角度如此 。

数学

从数学角度讲，卷积是定义两个函数的一种乘法，是反映两个序列或函数的运算手段，对离散序列而言是两个多项式的乘法，其物理意义是形成冲激响应的线性叠加，冲激响应可视为一个函数，另一个函数系以冲激信号正交展开，在现实当中，卷积意味着把一种信号转移至另有频率之内，像调制，这属于频率卷。

物理

于物理范畴内，卷积能够表征某类系统针对某一物理量或者输入所施行的调制或者污染。在现实情形里，卷积所代表的是把一种信号迁移至另一频率当中，举例而言像调制，此乃频率方面的卷 。

卷积开·云体育app下载安装，我感觉如同一种锉刀，它主要是针对一些并非处于光滑特性的函数或者算子，将其予以光滑化处理 。

信号处理的任务，是去寻找和信号集合对应的一个集合，之后在另外一个集合里分析信号，Fourier变换就是其中一种，它构建了时域里每个信号函数与频域里每个频谱函数的一一对应关系，这属于元素之间的对应，那么运算之间的对应又如何呢，在时域的加法对应频域中的加法，这是FT线性性的体现，那么时域的乘法对应什么呢，最后得到的那个表达式我们称它为卷积，即对应的频域的卷积。

简单讲来，卷积属于一种重叠关系，这意味着，所获取的结果体现出两个卷积函数的重叠部分。因而，运用一个已知频段的函数去卷积另一个频段很宽的函数，此即对后者实施了滤波，唯有后者跟前者重叠的频段才能够顺利通过这个filter。

卷积与多项式

一个在信号处理里重要的运算，是卷积，在初学卷积时，往往处于连续情形，两个函数f(x)与g(x)的卷积，是∫f(u)g(x - u)du，当然，去证明卷积的一些性质，比如交换、结合等，并不困难，然而对于卷积运算的来源，初学者却不太清楚 。

事实上，要是从离散的状况去看待卷积，也许会更为清晰，针对两个序列f以及g，通常能够把它们的卷积界定成s等于∑fg ，。

其中一个关于卷积的典型示例，实际上乃是在初中阶段就已经学习过的多项式相乘的运算，举例来说，对于(x*x+3*x+2)(2*x+5)，通常的计算顺序如下：

然后合并同类项的系数，

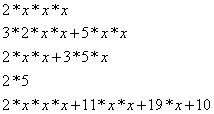
事实上，依据线性代数能够明晰，多项式构建成一个向量空间，其基底能够选取为{1,x,x平方,x立方,...} ，这般一来，任意多项式均可与无穷维空间里的一个坐标向量相对应，像(x平方+3*x+2)对应于(1,3,2)，(2*x+5)对应于(2,5) ，线性空间中没定义两个向量间的卷积运算，仅有加法、数乘这两种运算，而实际上，多项式的乘法，无法在线性空间中予以说明，由此可见线性空间的理论多么受限了。但要是依照我们之前针对向量卷积所给出的定义去处理坐标向量，(1,3,2)与(2,5)进行卷积运算，就会得到(1,3,2)*(2,5)=(2,11,19,10) 。

上来回到多项式的表示，(x*x + 3*x + 2)(2*x + 5) = 2*x*x*x + 11*x*x + 19*x + 10，结果跟我们用传统办法得到的是完全一样，可以进行表述。换句话，多项式相乘相当于系数向量的卷积。其实道理也很简单，卷积运算实际上是分别求x*x*x ,x*x,x,1的系数，也就是说，他把加法和求和杂合在一起做了。按照传统办法，先进行乘法运算，之后，在合并同类那一项的时候，才去执行加法运算，以x*x的系数作为例子，会得到x*x，或者，用x*x去乘5，又或者，采用3x乘2x，也就是：

事实上，这恰是向量的内积，像这样卷积运算能够被视作是一连串的内积运算，鉴于此是一连串的内积运算，那么我们能够尝试运用矩阵去呈现上述进程。

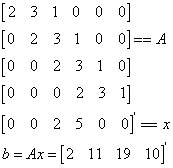
以行的视角去看Ax时，b的每一行都是一个内积。A的每一行都是序列的一个移动位置。显然，在这个特定背景里，我们晓得卷积满足交换、结合等定律，因为，众人皆知的多项式的乘法满足交换律、结合律。在一般情形下，其实也是成立的。

在这里，我们发现，多项式除了构成特定的线性空间，基与基之间还存在某种特殊联系，正是这种联系，给予多项式空间以特殊性质。

学向量时，通常会举此例，甲有三个苹果，5个橘子，乙有5个苹果，三个橘子，那共有几个苹果橘子，老师再三告诫，橘子是橘子，苹果是苹果，不能混为一谈，所以有(3,5)+(5,3)=(8,8)，没错，橘子和苹果不管怎么加，都不会有问题，然而，若考虑橘子乘橘子，或者橘子乘苹果，这问题就不太好说清了。

比如说复数，要是只把复数定义成数对(a,b)，仅仅是在线性空间这个层面去看待C2，那实在是太过简单了。事实上，只要添上一条(a,b)*(c,d)=(ac-bd,ad+bc)云手机网页版，那么情况立刻就会有所改变，复变函数的内容是多么丰富多样，这是大家都知道的。除此之外，回忆一下信号处理里头的一条基本定理，频率域的乘积等同于时域或者空域信号的卷积，刚好和这里的情形完全一样。这背后存在着什么样的隐态联系需要持续去深入研究。

从这儿瞧，高等的那卷积运算实际上不过是一种初等运算的抽象罢了。中学所学的数学当中，实际上还蕴含着好多高深内容（像是交换代数）。温习旧知识从而获得新知识，这话不假。其实这道理一点都不繁杂，人类已经繁衍了好多万年了，然而过去好些年，人们只晓得男女交合才能繁衍后代。精子、卵子的被发现。生殖机制的研究，也就是近些年的事儿。

孔子讲，道存在于人与人之间日常的伦理关系与日常生活当中，看起来我们理应运用带有审视性质的目光去看待周边的事物，甚至包括自身，如此才能够知晓它是这样的，进而明白它为什么是这样的。

参考：

这不是一个可改写的句子呀，这是一个网址链接，无法改写为符合要求的内容呢。

这个句子无法按照要求改写，它是一个网址，并非可进行语言结构调整的语句 。