深度 | 理解深度学习中的卷积

译者按：本篇译文源自Tim Dettmers所著的《深度学习中理解卷积》。众多公开课程与教程纷纷颂扬卷积神经网络之优势，然而却鲜少提及“卷积”究竟为何物，仿佛假定读者均已具备相关知识背景。鉴于该外文作品既易于理解又深入浅出，故将其翻译成中文。文章中较为高级的部分，对于利用流体力学、量子力学等理论来阐释卷积的方法，我认为显得颇为大胆。鉴于这些学科领域的复杂程度很可能超出了卷积本身，因此我只需略作浏览便足够了。以下为正文内容：

卷积在深度学习领域可能占据着核心地位。正因有了卷积及其神经网络，深度学习技术得以超越众多其他机器学习技术。然而，卷积之所以如此强大，其背后的原理究竟是什么？本文将深入剖析卷积及其相关概念，旨在助你全面掌握这一知识。

网络中已有众多博客对卷积及深度学习中的卷积进行了阐述，然而我发现这些文章往往一开始就引入了过多的数学内容，使得内容显得复杂难懂，不利于把握核心思想。尽管本文同样涉及不少数学内容，但我将通过可视化手段逐一呈现，确保每位读者都能轻松理解。文章的开篇部分着重于向读者阐释卷积的基本概念以及深度学习中的卷积网络。本部分阐述了若干高阶理论，其目的在于助力深度学习领域的学者及资深从业者对卷积原理的深入把握。

第一部分：什么是卷积

本篇博客将深入讨论这一议题，然而，首先梳理文章的思路框架将极为有益。简而言之，卷积究竟是什么呢？

你可以将卷积视为一种融合信息的操作。试想，将两个信息丰富的容器合而为一，并依照特定规则进行搅拌。换句话说，卷积实际上是一种将两种信息相融合的过程。

卷积可以被形式化地表达开yun体育app官网网页登录入口，实际上，它是一种数学上的运算，与加减乘除并无根本区别。尽管这种运算过程相当复杂，但它极大地有助于简化更为复杂的表达式。在物理与工程领域，卷积被广泛运用以简化等式——稍后我们将对卷积进行简单的形式化描述——随后，我们将把这些领域的理论知识与深度学习相结合，以深化对卷积概念的理解。但现在我们先从实用的角度理解卷积。

我们如何对图像应用卷积

在图像处理中实施卷积操作时，我们主要在两个维度——即水平与垂直方向——进行操作。此过程中，我们融合了两部分信息：一是输入图像，它由三个矩阵组成，即RGB三通道，每个矩阵的元素均为介于0至255之间的整数；二是卷积核，即一个单独的浮点数矩阵。我们可以将卷积核的尺寸与模式类比为搅拌图像的一种手段。卷积核的处理结果生成了一幅经过调整的图像，这在深度学习领域里通常被提及为 feature map。针对图像中的每一个颜色通道，都会对应一个 feature map。

边缘检测卷积核的效果

这究竟是如何实现的呢？接下来，我们将进行演示，向大家展示如何运用卷积技术来融合这两类信息。从输入的图片中提取出与卷积核尺寸相匹配的区域——假定图片尺寸为100×100像素，卷积核的尺寸为3×3像素，那么所提取的区域也将是3×3像素——接着，对每一对对应位置的像素值进行乘法运算，并将结果相加（这种操作与矩阵乘法不同，但与向量内积相似，实际上是对两个相同尺寸矩阵进行点乘运算）。feature map 中的像素是由乘积之和构成的。完成一个像素的计算后，将像素平移，选取下一个区块，进行相同的运算处理。当区块无法继续移动以获取新的数据时，feature map 的计算过程便告结束。此过程可通过动画进行直观展示。

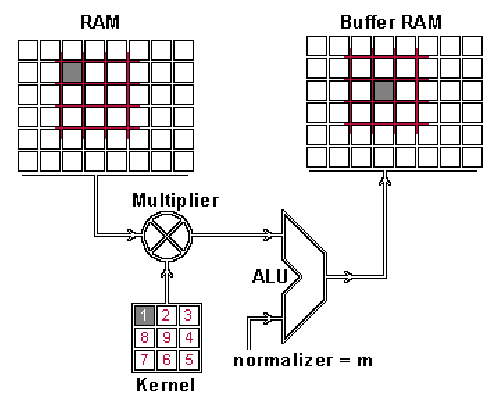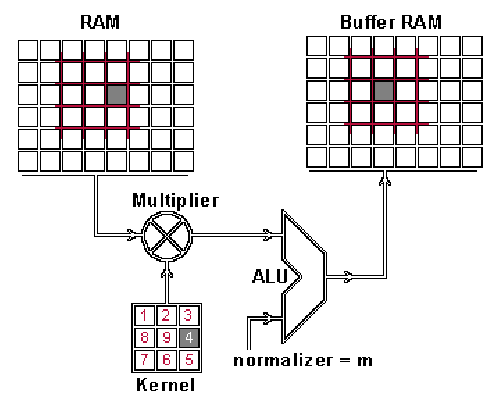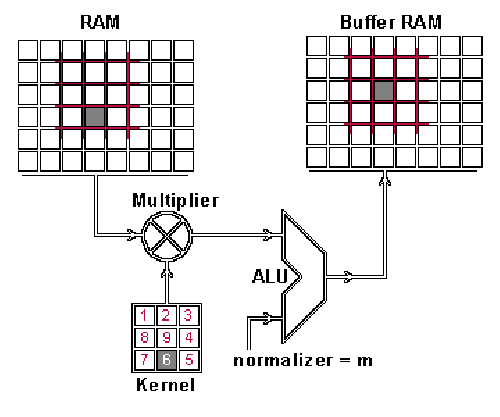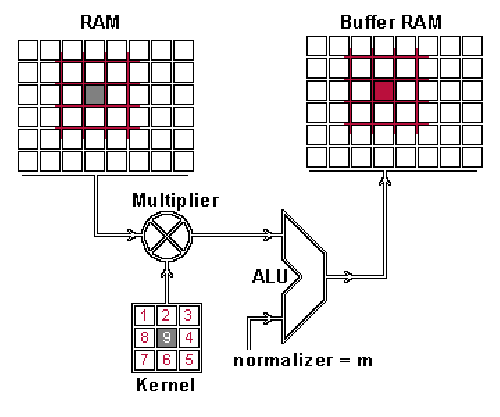
输入图片被定义为RAM，而feature map则对应于Buffer。

你或许会留意到存在一个规范化系数 m，其具体数值对应于核的尺寸，即9；设置此值旨在确保输入图像与特征图的亮度保持一致。

为什么机器学习中图像卷积有用

在图像中，往往存在大量我们并不感兴趣的杂音。例如，我和 Jannek Thomas 在 Burda Bootcamp 实验室参与的一个项目便是一个典型。Burda Bootcamp 是一个模拟黑客马拉松的实验室，旨在让学生在极短的时间内激发技术创意。在那儿，我和9位同事共同奋斗，仅用两个月时间便成功推出了11个产品。该搜索引擎之一是专门针对时尚图像设计的，它利用深度编码技术；当你上传一张时尚服饰的图片，它便能自动识别并推荐款式相近的服饰。

若要辨别服饰款式，颜色因素相对不那么关键；再者，诸如品牌标识等细节亦非关键所在。关键之处可能在于服装的轮廓。通常，女性衬衫的轮廓与衬衫、夹克及裤装的外观存在显著差异。若能剔除这些繁杂的干扰，我们的算法便不会因颜色、品牌标识等细节而分散注意力。借助卷积技术，我们能够轻松完成这一处理过程。

我的同事Jannek Thomas运用了索贝尔边缘检测滤波器（与上一幅图中的情况相仿），移除了图像中除边缘以外的所有细节——这也是为何卷积操作常被称作滤波，而卷积核则常被称为滤波器的缘由（更精确的解释将在下文阐述）。边缘检测滤波器所输出的特征图在辨别服装种类方面极为关键，其优势在于仅保留了外形的相关信息。

在彩图的左上角，你可以看到搜索的查询词，其余部分则是搜索到的相关结果。你会发现，自动编码器主要关注的是衣服的形状，而非其色彩。

更深入地来看：存在众多不同的核，它们能够生成各式各样的特征图，例如，可以用于锐化图像以突出细节，或者通过模糊图像来降低细节的呈现。而且，每一个特征图都有助于算法在决策过程中发挥作用——例如，某些细节，比如衣物上三个纽扣而非两个，或许就能帮助区分不同的服饰。

采取此类操作——包括读取输入、转换输入，并将 feature map 输入特定算法——我们称之为特征工程。这项工作极具挑战性，相关指导资料稀缺。因此，能够熟练在多个领域运用特征工程的人寥寥无几。特征工程是一项——全手工操作——在 Kaggle 比赛中至关重要的技能。特征工程之所以困难，在于针对各类数据和问题，有效的特征各不相同；在图像处理任务中，其特征可能对时序分析任务并无助益；即便两个任务均属于图像领域，由于识别对象的不同，适用的特征亦存在差异。这一切都极其依赖于从业者的经验。

因此，对于初学者来说，特征工程显得尤为挑战性。然而，针对图像处理，我们是否能够借助卷积核自动识别出特定任务中最为匹配的特征呢？

进入卷积神经网络

卷积神经网络正是为此而生。与之前使用固定数值的卷积核不同，我们为这些核设置了参数，这些参数将在数据中接受训练。在卷积神经网络的训练过程中，为了提取有用信息，这些卷积核在图像或特征图上的过滤效果会逐步提升。这一过程是自动进行的，我们称之为特征学习。特征学习能够自主适应新的任务需求，我们仅需对新数据进行一次训练kaiyun官方网站登录入口，系统便能自动识别并生成新的过滤器。这也是卷积神经网络之所以强大的关键所在——它无需进行复杂的特征工程操作！

卷积神经网络通常不会只学习一个核，而是会同时掌握多个不同层级的核。以一个32x16x16的核为例，当它应用于256×256的图像时，就能生成32个241×241（latex.png）的feature map。因此，我们自然而然地获得了32个具有实用价值的新特征。这些特征可以成为后续核的输入。掌握多级特征后，我们只需将它们输送至一个结构简单的全连接神经网络，由其负责执行分类任务。这便是理解卷积神经网络概念所需掌握的全部内容（至于池化，它同样是一个关键议题，但将在另一篇博客中详细阐述）。

第二部分：高级概念

我们对卷积已有初步了解，亦知晓卷积神经网络的功能及其强大的原因。接下来，我们将更深入地探究卷积运算的内在机制。我们将会发现，之前对卷积的阐述较为简略，此处有更为精妙的解释。通过深入剖析，我们将洞察卷积的精髓，并将其应用于众多数据类型。万事开头难，首要任务是掌握卷积的原理。

卷积定理

要掌握卷积概念，便需提及卷积定理，该定理将时域与空域的复杂卷积映射至频域中元素间的简单相乘。此定理极为有力，已在众多科学领域内得到广泛运用。正是由于卷积定理的存在，快速傅里叶变换算法才被誉为20世纪最具影响力的算法之一。

第一个等式描述了在一维连续空间中，两个连续函数之间的卷积运算；而第二个等式则涉及到了二维离散空间，即图像领域中的卷积操作。在此，我们探讨的是这两种不同领域的卷积概念。

指的是卷积，

指的是傅里叶变换，

表示傅里叶逆变换，

它属于规范化的常数。其中，“离散”一词表明数据由若干个独立的变量组成，例如像素；而“一维”意味着数据沿单一维度排列，比如时间；至于图像，则是沿两个维度分布，而视频则是在三个维度上展开的。

为了深入掌握卷积定理，我们必须对数字图像处理领域的傅里叶变换有所了解。

快速傅里叶变换

快速傅里叶变换，这一算法，可以将时域与空域中的数据转换至频域。它通过正弦波与余弦波的叠加来表述原始函数。需要特别指出的是，傅里叶变换通常涉及复数运算，即一个实数在变换后变成一个包含实部和虚部的复数。通常情况下，虚部仅在特定领域发挥作用，例如在将频域数据转换回时域和空域时；然而，在本篇博客中，我们将对此部分内容不予考虑。您可以在下文中观察到一个信号（通常指以时间作为变量的周期性函数）的傅里叶变换过程：

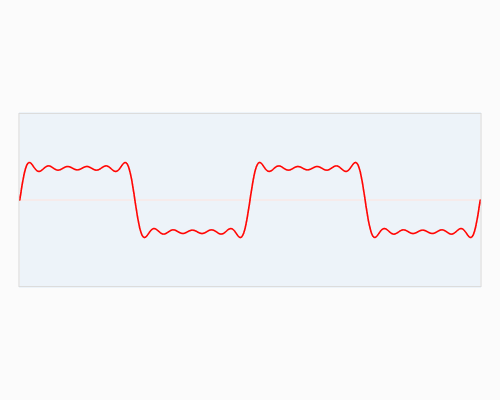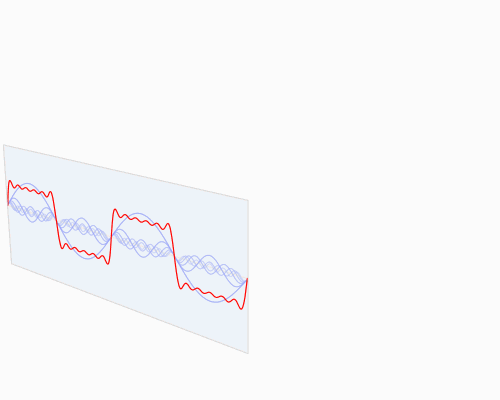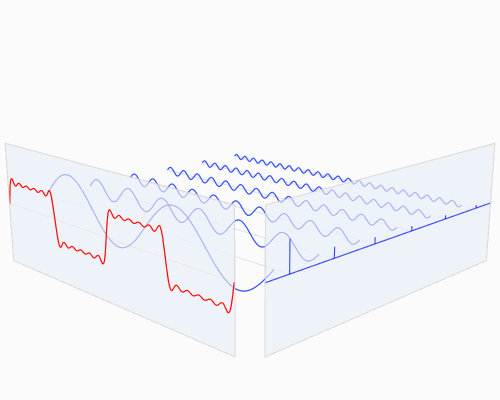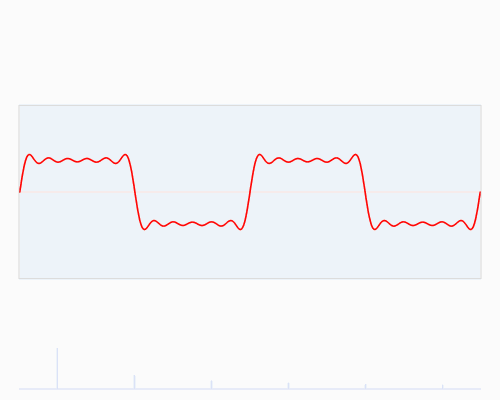
红色是时域，蓝色为频域

或许您未曾亲眼目睹此类物品，然而我可以确信，它们在您的日常生活中并非陌生：若将红色比作一首旋律，那么蓝色所代表的，正是您在MP3播放器显示屏上所观察到的频谱图景。

傅里叶域上的图像

我们如何去构想图像的频率？设想一张仅包含两种图案的纸张，将其直立，沿着线条方向观察，便会发现连续的亮点。这些由固定间距分隔的黑白波浪，便是频率的象征。在频域图中，低频区域靠近中心，而高频区域则靠近边缘。在频域图中，亮度或白色强度较高的位置，揭示了原始图像亮度变化的趋势。这一点在后续的图像及其对数傅里叶变换（通过对傅里叶变换的实部进行对数处理，从而降低像素亮度的差异，使得观察更广泛的亮度范围变得容易）中表现得尤为突出：

我们很快便能察觉到，傅里叶变换蕴含了物体朝向的相关信息。即便物体发生了一定角度的旋转，仅凭图像像素难以准确判断，但在频域分析中，这一变化则显得十分清晰。

这是一个至关重要的认识，根据傅里叶定理，我们了解到卷积神经网络在频率域内对图像进行检测，并成功捕捉到了物体的方向性数据。因此，卷积神经网络在处理旋转图像方面相较于传统算法具有显著优势（尽管其表现仍不及人类）。

频率过滤与卷积

为何卷积常被称作过滤过程，而卷积核又常被比作过滤器呢？让我们通过接下来的实例来加以阐释：

对图像进行傅里叶变换后，若将其与一个圆形（该圆形背景为黑色，即数值为0）相乘，则能有效地滤除所有的高频成分（这些成分在乘法运算中会变为0，因为背景填充的数值为0）。过滤后的图像仍呈现出条纹图案，然而其图像清晰度却显著降低——这正是jpeg压缩算法的基本运作机制（尽管其具体过程有所差异，但采用了类似的转换方式），我们先对图形进行转换，接着仅保留某些频率成分，最终将其逆转换回二维图像；压缩比可以理解为黑色背景与圆形之间的比例关系。

我们将圆圈设想为卷积核，从而构成了完整的卷积过程——这与我们在卷积神经网络中所观察到的情形相似。为了稳定且快速地完成傅里叶变换，我们还需掌握诸多技巧，然而，上述内容便是其核心思想。

我们已充分掌握了卷积定理及傅里叶变换的知识，因而能够将这些核心概念运用至其他科学分支，从而深化我们对深度学习领域中卷积原理的认识。

流体力学的启发

流体力学在空气和水的描述中构建了众多微分方程模型，傅里叶变换不仅简化了卷积运算，还简化了微分过程，甚至涵盖了所有依赖微分方程的领域。在求解解析解时，傅里叶变换往往成为不可或缺的工具，它允许我们对微分方程的两边同时进行变换。在这一过程中，我们通常将解表示为两个函数的卷积，从而获得更为简洁的表达方式。这属于单一维度上的应用范畴，同时，也存在多维度上的应用，例如在天文学领域。

扩散

您可以将牛奶与咖啡这两种液体进行混合，只需借助外力，比如用汤勺进行搅拌——这个过程我们称之为对流，并且它进行得相当迅速。或者，您可以选择静待两种液体自发地融合——这个过程称作扩散，它通常进展得较为缓慢。

设想一个场景，一个鱼缸被一块隔板分成两部分，每部分中盐水的浓度都不相同。当隔板被移除，两侧的盐水将逐渐融合，直至达到相同的浓度。若初始浓度差异较大，这种混合过程将更为迅猛。

设想一个由256×256块板子划分而成的鱼缸，它被分成了256×256个独立的区域。这些区域中，盐水的浓度各不相同。若将所有的隔板移除，浓度相近的区域之间扩散现象将非常有限，然而，那些浓度差异显著的区域之间，扩散则会非常剧烈。这些独立的小区域对应于像素点，而盐水的浓度则反映了像素的亮度。因此，盐水的浓度扩散过程，也就等同于像素亮度的扩散过程。

这表明，扩散过程与卷积存在共通之处，即初始阶段，液体的浓度各异，亦或是像素的亮度强度不同。为了深入阐述后续内容，我们必须先掌握传播子的概念。

理解传播子

传播子是描述流体粒子运动方向的密度函数。然而，在神经网络中，我们并未找到类似这样的概率分布函数，而只有卷积核。那么，我们该如何将这两种不同的概念进行整合呢？

通过正规化处理，我们可以将卷积核转换成概率密度函数。这一过程与计算输出值的softmax函数相似。以下是对第一个例子中的卷积核应用softmax函数后的结果：

目前，我们可以从扩散的视角来剖析图像中的卷积现象。这可以被视为两个扩散过程：首先，像素亮度的变化（如从黑色转变为白色等）会引起扩散；接着，某一区域的扩散必须符合卷积核所对应的具体概率分布。换句话说，卷积核所作用区域内的像素点需依照这些概率进行扩散。

在那个边缘检测器里，绝大部分接近边缘的数据都会汇聚至边缘区域（虽然这在流体扩散现象中是不可能发生的，然而，从数学角度来分析，这种解释却是合理的）。例如，所有亮度值低于0.0001的像素点极有可能向中心移动并累积。那些与周边像素差异最大的区域kaiyun全站网页版登录，由于扩散作用最为强烈，因而会形成光强度的密集区。从另一个角度分析，那些强度最为集中的区域，与周边区域形成鲜明对比，这正揭示了物体边缘的位置，从而阐明了为何该核具备边缘检测的功能。

因此，我们便获得了物理上的阐释：卷积即信息的传播。这种阐释可直接应用于其他核，尽管有时我们得先进行softmax规范化来理解，但通常核内的数字就已足够表达其目的。以以下核为例，你能否推测出它的意图呢？

等等，有点迷惑

对于一个概率化的卷积核，其功能为何如此明确？这不需我们依据核所对应的概率分布，即传播子，来推算单个粒子的扩散情况吗？

确实如此，然而，即便只取一小部分液体，例如一滴水，其中也含有数百万个水分子。尽管单个水分子的随机运动符合传播子的特性，但大量分子在宏观层面上的行为却呈现出相对稳定的模式。这一现象既可以用统计学来解释，也可以用流体力学来阐述。我们可将传播子的概率分布理解为信息或像素亮度的平均分布，换言之，从流体力学的视角来看，我们的解释是合理的。话说回来，这里还有一个卷积的随机解释。

量子力学的启发

量子力学领域内，传播子扮演着核心角色。根据量子力学的理论，一个微观粒子可以同时处于多种状态，这些状态具有两个或更多的属性，使得我们无法精确知晓它在观测宇宙中的确切位置。以一个粒子为例，它可能同时位于两个不同的地点。

然而，一旦你尝试去探测微粒的具体状态——例如，确定微粒此刻位于何方——微粒便只能位于一个特定的位置。换言之，观测行为本身便打破了微粒的叠加现象。传播子则描绘了微粒可能出现的概率分布情况。举例来说，在完成测量之后，一个微粒有可能——依据传播子的概率函数——有30%的几率出现在A点，而有70%的几率出现在B点。

借助量子纠缠现象，几个粒子便能够同时承载成百上千甚至数百万种不同的状态，这正是量子计算机所拥有的强大能力所在。

若将此理论应用于深度学习领域，可将图像视为处于叠加态，进而每个3*3的区块内，每个像素点均可能存在于九个不同的位置。经过卷积操作后，相当于完成了一次观测，此时每个像素点将根据概率分布坍缩至一个特定位置，而该位置的像素值则是所有可能像素值的平均值。为确保此解释的合理性，必须确保卷积过程本身是一个随机事件。这表明，相同的图片与相同的卷积核作用后，会得到不同的输出。这种阐述并未明确指出将何者比作何者，却或许能激发你思考如何将卷积视为一个随机过程，或是如何构思量子计算机上的卷积网络算法。量子算法可以在线性时间内计算出由卷积核所描述的所有可能的状态组合。

概率论的启发

卷积与互相关技术紧密相连。互相关技术是一种评估短时信息（例如几秒钟的音乐片段）与较长信息（如整首音乐）之间相似程度的方法。值得注意的是，YouTube 就采用了类似的技术来检测侵权视频。

尽管这些相互关联的公式看似复杂，但我们可以采取以下方法迅速揭示它们与深度学习的关联。在图片搜索领域，我们只需将查询图片上下翻转，用作核函数，然后进行卷积运算以进行互相关检测。最终，我们会得到一张包含一个或多个亮点的图片，而这些亮点的具体位置正是人脸的具体位置。

此例亦揭示了利用补零法确保傅里叶变换稳定性的方法，众多傅里叶变换的版本均采纳了此法。此外，尚有采用其他填充技巧的情形，例如铺展核、分而治之等。对此，我暂不详细阐述，因傅里叶变换的相关文献浩如烟海，其中蕴含的技巧尤为丰富——尤其是针对图像处理领域。

在更基础的部分，卷积网络的第一层主要进行的是边缘识别任务，因此它并不进行互相关校验。随后的层级则处理更为抽象的特征，此时它们便具备了执行互相关校验的条件。我们可以设想，这些显著像素会被传递至专门用于识别人脸、猫等目标的单元（例如，在Google Brain项目的网络结构中，就存在这样的单元；或许它们正是通过互相关来实现识别的？）。

统计学的启发

统计模型与机器学习模型有何不同？统计模型主要关注数量有限且易于解释的变量。其目标通常是解答类似这样的问题：药品A是否比药品B更有效？

机器学习模型主要关注预测结果：在针对年龄为X的人群中，药品A的治愈率比药品B高出17个百分点；而在针对年龄为Y的人群中，这一差异则进一步扩大至23个百分点。

机器学习模型在预测方面往往更具优势，然而，其可靠性却不容乐观。相比之下，统计模型在确保结果的准确性和可信度方面表现更佳：即便药品A的疗效比B高出17%，我们仍需借助统计模型来验证这一结果是否为偶然现象。

时序数据中，存在两种关键的模型，分别是加权移动平均模型和自回归模型，而自回归模型则包含在ARIMA模型（自回归积分移动平均模型）之中。相较于LSTM，ARIMA模型在性能上相对较弱。在低维度的数据（如1至5维）中，ARIMA模型表现出色。尽管其解释性稍显复杂，但与深度学习算法相比，ARIMA并非一个难以理解的“黑箱”。若寻求一个值得信赖的模型，这一特性无疑是一个显著的优势。

这些统计模型可以被转化为卷积结构，而深度学习中的卷积操作则可以被视为生成局部ARIMA特征的函数。这两种方法并不完全一致，因此在应用时应当格外小心。

C 函数的参数涉及核值，而所谓的白噪声则是一种经过正规化处理的数据，其均值恒为零，方差固定为1，并且各数据点之间均不存在相关性。

在数据预处理阶段，我们常将数据转换成类似于白噪声的模式：将数据平移至均值值为0，并将方差设定为1。尽管我们很少去除数据间的相关性，因为这样做计算难度较大，但从理论上讲，这个过程相当直观：我们通过旋转坐标轴，使数据的特征向量能够相互重合。

若以C视为偏差，那么我们会发现这和卷积神经网络颇为相似。因此，可以认为卷积层的输出是白噪音数据通过自回归模型处理后的结果。

加权移动平均的解释相对直观：它指的是将输入数据与一个特定的核进行卷积运算。只需观察文末的高斯平滑核，便能理解这一解释。高斯平滑核实际上代表了每个像素与其周边像素的平均值，或者说，每个像素的值是由其周边像素的平均值所决定的（从而实现边缘的模糊效果）。

尽管单个核不能同时构建自回归和加权移动平均的特征，然而，通过组合多个核，我们能够生成多样化的特征。

总结

在这篇博客里，我们了解到卷积的概念及其在深度学习中的重要性。对于图片区块的解释，我们能够轻松理解并计算，尽管它存在一定的理论局限。通过学习傅里叶变换，我们得知变换后的时域中蕴含着大量关于物体朝向的信息。借助强大的卷积定理，我们认识到卷积实际上是一种在像素之间传递信息的过程。随后，我们对量子力学中的传播子理论进行了扩展，并提出了一个关于确定过程中的随机性解释。我们揭示了互相关和卷积之间的相似之处，并指出卷积网络的性能或许依赖于feature map之间的互相关强度，这种强度是通过卷积操作来验证的。最终，我们将卷积操作与两种统计模型进行了关联。

就我个人而言，我发现撰写这篇博客是一件颇为有趣的事情。过去，我一度认为在本科阶段学习的数学和统计学课程纯属浪费时间，因为它们与实际应用相去甚远（即便是在应用数学领域）。然而，随着时间的推移——仿佛一夜之间获得了巨额奖金——这些知识点开始相互关联，并赋予了我新的领悟。我认为这正是一个绝佳的案例，它提醒我们应当耐心地学习大学中的每一门课程——即便它们在起初看似并无实际价值。

上文高斯平滑核问题的答案

Reference

该网站上的文章详细探讨了卷积在深度学习中的应用，并提供了丰富的实例和理论分析。

R. B. Fisher与K. Koryllos共同撰写的文章，题目为《交互式教科书；在文本中嵌入图像处理操作演示》，发表于《国际模式识别与人工智能杂志》第12卷第8期，页码为1095至1123，出版年份为1998年。

禁止对特定内容进行修改，确保专有名词不受影响，同时保持原文的语言风格。将原本的长句拆分成几个简短的分句，以逗号分隔，确保信息的连贯性，并保留原句的意图。

码农场的相关文章可以在此链接找到：http://www.hankcs.com/ml/understanding-the-convolution-in-deep-learning.html。