我才知道，原来职场处世有妙计，36 计超实用，助力职场人游刃有余
天呐，太厉害了，快五十时才知悉竟然是此般状况 于这职场之中混得相当出色之人 早就将处世那三十六计能够宛如倒着背那般知晓得清清楚楚了 看过过后真切是被那种厉害程度深深地惊艳住了 像啥施思计或是迂回计 还有捧杀计以及借口计 亦有着贴金计和把柄计 并有装傻计以及退让计之余 更有那自嘲计和观色计以及最后的走为上计 要...
生活应用 第43页
浅析勾股定理在生活中的应用研究
浅析勾股定理在生活中的应用研究
周飞玲
勾股定理出自生活，它表明直角三角形三边的数量关联，运用数形结合方式把勾股定理用到实际生活里头，解决实际问题.
一、引言
从古到今，人们对于勾股定理的证明十分踊跃，积极参与，勾股定理如同几何学里的明珠一般，距离探究勾股定理业已有将近四千年的时光历程存在，当前大约拥有500...
三十六计之瞒天过海：现代生活中的智慧与策略
引言：古代智慧在现代的应用
古代智慧所具魅力，每每在于那跨越时空之策略以及思考方式。瞒天过海这古老策略，今时依旧有重要参考价值，如今已把它融入现代社会好些领域。于商业决策阶段之中，瞒天过海智慧展现在公司经由多方手段来隐藏真实意图，借此在竞争里占有先机；于人际交往过程当中，众人时常拿瞒天过海用以保护自分，防止被...
三十六计新坐标：三十六计离我们很近，也很容易理解
昨天竹判官发表了一篇题为《三十六计新坐标之不殆之道》的文章， 此篇作为《三十六计新坐标之... 返回主贴 • 发 的系列文章起始篇第一篇。此后发现有些读者提出反馈称文内内容表述深邃难懂，颇具费解之象不大容易让读者轻易明白和理解。今日为了能够对... 便于诸多方便和更大便利诸多普通读者去展开继续阅读该系列文章，...
勾股定理的实际应用：解析生活中的几何问题
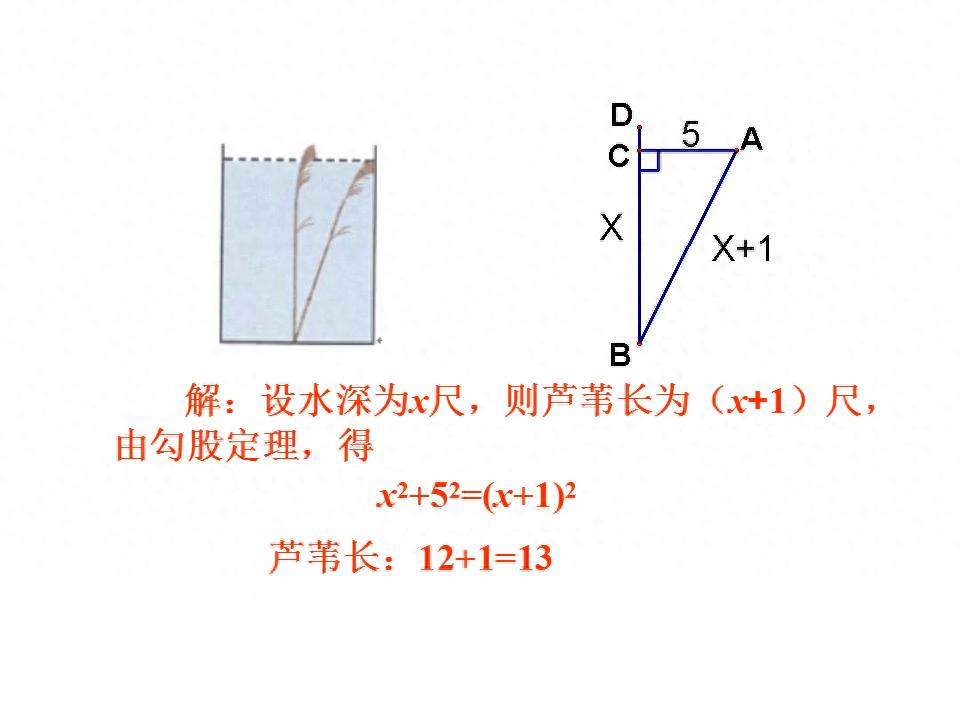
在日常日子当中，我们时常碰到各类各式的几何难题，可是勾股定理却是解决这些疑难问题的充满力量的有用工具。勾股定理是一个年代久远而且关键重要的数学原理准则，其表述为直角三角形的两条直角边的平方之和等同于斜边的平方这么一种情况。这么一来，我们究竟该怎么样去运用勾股原理来让生活层面的几何问题得到简化呢。
其一，知晓勾...
从军事到职场，三十六计如何成为人生指南
这一我国古代有关兵学之精髓的东西被叫做三十六计，该精髓当中的要点等被誉为具有很高超又独到益智方面的丰富精华、非常卓越精巧谋略方面的全部成就集成汇合在了一块儿，蕴藏深厚不偏不倚这样精当特别有理辩证哲理，不仅大力给予支持让全中华民族始终站立不败在世界的那种展示平台上面，更加生成变成在人类各类领域范围当中能够挫败...
勾股定理在实际生活中的应用
勾股定理第2课时。
勾股定理在实际生活中的应用。
学习目标：
1.会运用勾股定理的数学模型解决现实世界的实际问题。
2. 判定定理是，直角三角形全等的“斜边、直角边”判定定理，而此可用勾股定理来进行证明。
3.经历把实际问题转化成数学问题，利用勾股定理解决的过程。
请你明确一下问题哦，你给出的内容感觉不太完整...
勾股定理在现实生活中有哪些应用
勾股定理在现实生活的应用有这些方面
从事工程技术工作的人员运用勾股定理的情况较为频繁，像是农村建造房屋时其屋顶的构造，能够借助勾股定理展开计算，进行工程图纸设计的过程也要使用勾股定理，在求取和圆、三角形有联系的数据之际，大多能够运用勾股定理。
在物理范畴之中有着广泛的应用实例，比如说求解几个力，又或者是研究物...
17.1.2 勾股定理在实际生活中的应用 同步练习 （含答案）2024-2025学年人教版八年级数学下册
资源简介
17.1.2 勾股定理在实际生活中的应用
中小学教育资源及组卷应用平台
知识要点分类练夯实基础
知识点 1 勾股定理的一般应用
如图17 - 1 - 10所示，存在一处情形，即为了能够精准测出湖两岸A与B之间的距离，观测者会在C处预先设置桩点，从而致使ABC恰好构成一个直角三角形，其中∠ABC等于...
华南理工大学科研团队提出一种新型感应式耦合电能传输系统
在无线电能传输系统里，一旦松耦合变压器的参数固定，并且补偿电路的参数也固定之后，感应式耦合电能传输（Inductive Coupled Power Transfer, ICPT）变换器固有的电流源输出特性不可调，其电压源输出特性同样不可调，所以输出电压范围受限，而且输出电流范围也受限，在实际应用层面仍旧存在很...