17.1.2 勾股定理在实际生活中的应用同步练习（含答案）2024-2025学年人教版八年级数学下册

频道：生活应用日期：2025-10-27 01:04:38 浏览：6

资源简介

17.1.2 勾股定理在实际生活中的应用

中小学教育资源及组卷应用平台

知识要点分类练夯实基础

知识点 1 勾股定理的一般应用

如图17 - 1 - 10所示，存在一处情形，即为了能够精准测出湖两岸A与B之间的距离，观测者会在C处预先设置桩点，从而致使ABC恰好构成一个直角三角形，其中∠ABC等于90°。经过一番细致测量，得以知晓AC的长度为10km，BC的长度则为8km，那么在此种状况下，A与B之间的距离究竟是( )

A. 8kmB.6 km C.10 km D.11 km

若有这样一幅图，其编号为17 - 1 - 11 ，图中有一棵规模较大的树木，在一场极为强大的台风侵袭过程当中，出现了折断并且倒下的情况，这棵大树在折断之前的整体高度是18米，当它倒下之后，树顶所处的位置距离大树根部是12米，那么请问这棵大树是在距离地面多少米的地方发生了折断答案为( )

A.3 B.4 C.5 D.6

如图17 - 1 - 12所示，有一根电线杆，在离地面12米之处，各用15米长的铁丝往两侧地面进行拉线固定，那么两个固定点之间的距离是

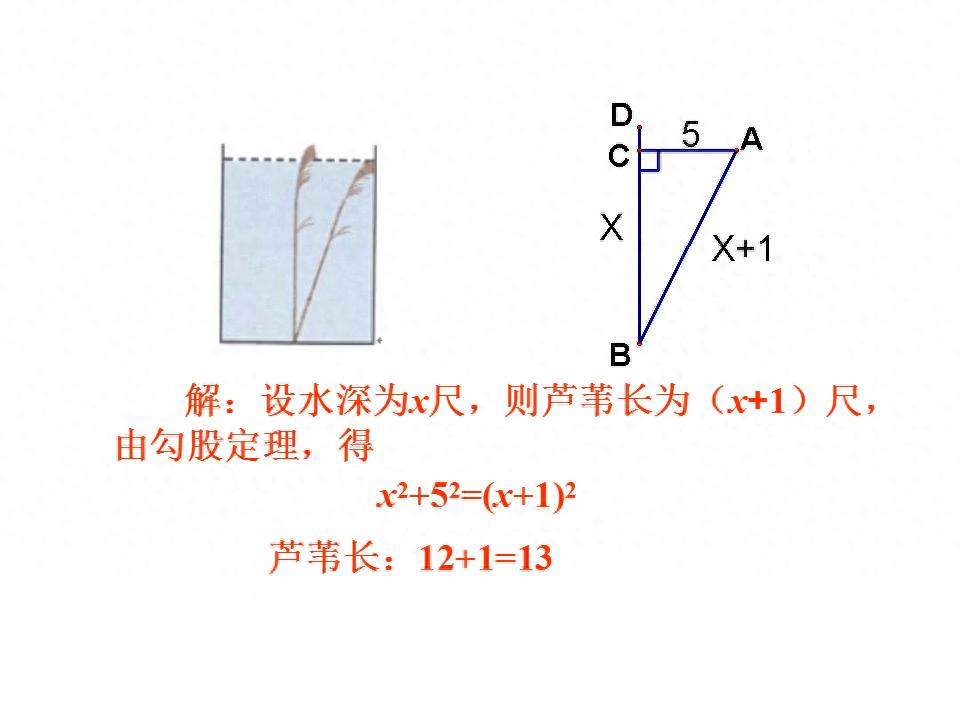
如图17 - 1 - 13，在数学活动课上，老师组织同学们进行测量，测量的对象是学校旗杆的高度AC，同学们发现一种情况，就是将系在旗杆顶端的绳子拉直垂到地面后还多1米呀，之后同学们又把绳子的末端拉开5米，这时发现绳子末端刚好接触地面，要求回答求旗杆的高度是多少呢(旗杆顶端滑轮上方的部分忽略不计)。

知识点 2 平面直角坐标系中勾股定理的应用

如图十七减一减十四，于平面直角坐标系当中，ABC各顶点坐标分别是A（一，二），C（五，二），B（五，四），那么AB的长度是.

若处于平面直角坐标系里，点P的坐标是(m减去2，4)，该点到坐标原点的距离为5，那么m的值是

知识点 3 梯子问题

在图17 - 1 - 15里，有一架梯子AB，它的长度是2.5米，此时这架梯子斜放在一竖直的墙AO上。

kaiyun官方网站登录入口，则这个梯子的顶端A 距地面有多高

在条件(1)的状况之下，若梯子顶端出现下滑了0.4米这种情况，那么梯子底端在水平方向所滑动的距离是几米呢？

规律方法综合练训练思维

首先，我们知道这是一个圆柱形饮料罐，其底面半径是5，高是12kaiyun全站登录网页入口，并且上底面中心有一个小圆孔。然后，要求的是一根到达底部的直吸管在罐内部分的长度a，这里罐壁的厚度和小圆孔的大小忽略不计。那么，当吸管垂直于底面放置时，此时在罐内部分的长度就是圆柱的高，即12。而当吸管斜着放置且与底面直径和圆柱的高构成直角三角形时，根据勾股定理，底面直径为2×5 = 10，此时斜着放置的吸管长度就是直角三角形的斜边，其长度为根号下（10的平方 + 12的平方），也就是根号下（100 + 144），等于根号下244，化简为2倍根号61。所以，一根到达底部的直吸管在罐内部分的长度a（罐壁的厚度和小圆孔的大小忽略不计）的取值范围是12≤a≤2倍根号61。

A.12≤a≤13 B.12≤a≤15

C.5≤a≤12 D.5≤a≤13

在有一个秋千示意图的情况下，其静止时踏板离地垂直高度为\(DE = 0.5m\)，往前推送\(3m\)即水平距离\(BC = 3m\)时，此时秋千踏板离地垂直高度为\(BF = 1.5m\)，并且秋千绳索一直拉得很直，那么求秋千绳索\(AD\)的长度为\(m\) 。

10.有一根长度是7cm的木棒，要把它放进一个长方体木箱里，这个长方体木箱的长是5cm、宽是4cm、高是3cm，问是不是能放进去.

11. 下面是一个“荷花问题”：

平平湖水清可鉴开yun体育app官网网页登录入口，面上半尺生红莲.

出泥不染亭亭立，忽被强风吹一边.

渔人观看忙向前，花离原位二尺远.

能算诸君请解题，湖水如何知深浅

请你用学过的数学知识回答这个问题.

1.有个B，2.存在C，3.其长度是十八米，4.还有十二米那么长，5.存在数字2，6.数字是5或者-1 。

7. (1)2.4 米 (2)0.8米 8. A