勾股定理在现实生活中有哪些应用

勾股定理在现实生活的应用有这些方面

从事工程技术工作的人员运用勾股定理的情况较为频繁，像是农村建造房屋时其屋顶的构造，能够借助勾股定理展开计算，进行工程图纸设计的过程也要使用勾股定理，在求取和圆、三角形有联系的数据之际，大多能够运用勾股定理。

在物理范畴之中有着广泛的应用实例，比如说求解几个力，又或者是研究物体的合速度，以及其运动方向 。

古代也是大多应用于工程，例如修建房屋、修井、造车等等

例1：

我国战国时期，另有一部古籍，名为《路史后记十二注》，其中有着这样的记载，“禹治洪水kaiyun全站网页版登录，决流江河，望山川之形，定高下之势，除滔天之灾，使注东海，无漫溺之患，此勾股之所系生也。”这段话其意思是这样说的，大禹为治理洪水，使不决流江河，依据地势高低，决定水流走向，因势利导kaiyun.ccm，让洪水注入海中，不再有大水漫溺的灾害，是应用勾股定理的结果。

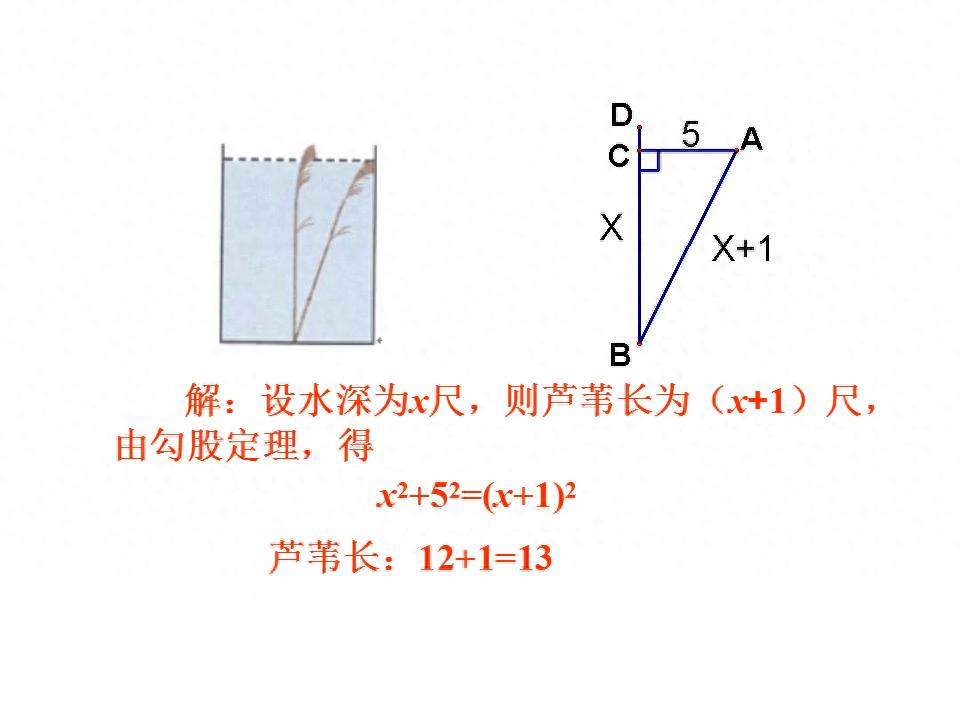
例2：

家居装修的时候，干活的工人，为了去判定一个墙角是不是标准的直角这种情况，能够分别在墙角朝着两个墙面方向量出30厘米，40厘米的长度并且在一个特定点儿做标记，接着量这两个标记点之间的距离是不是50厘米那么长。倘若超出限定的一定误差范围，那就表明墙角不是直角形状。

比如，在A位置存在一根立于高处的杆子，在其临近位置安排为B位置，要将从杆的顶端引下来的绳索固定于这个限定点，是能够计算出绳索长度所需条件的了。

例3：

如果在进行木工工作的时候，存在大块板材需要确定直角的情况，那就运用勾股定理。因为角尺尺寸过小，所以在大板面上所画的直角便会产生较大误差。当从事焊工活计时，制作大型框架，出现必须是直角的情形同样会运用勾股定理。举例来说，若需要一个直角，选取一条直角边为3米，另一条直角边为4米，使得斜边为5米，那么这个角便是直角了。这样一来，勾股定理在木工制作和焊工框架搭建中，对于确定直角起到了重要作用。

勾股定理的由来：

《周髀算经》称，夏禹于实际测量里已初步运用此定理，该书记载，存在一位叫陈子的数学家，运用此定理测量太阳高度，和太阳直径以及天地长阔等 。

5000年前的埃及人，晓得这一定理的特例，即勾3、股4、弦5，还用以测定直角，之后才逐渐推广至普遍情形，金字塔底部四正四方，严格对准东西南北，方向测量极为精准，四角为严格直角，量得直角可采用作垂直线之法，但将勾股定理反过来，就是只要三角形三边是3、4、，或者符合公式，那么弦边对面的角定是直角。在公元前540年的时候，希腊数学家毕达哥拉斯留意到，当直角三角形三边是3、4、5，或者是5、12、13的时候，有一种这样的关系，他思索着，是不是所有直角三角形的三边都契合这个规律呢？反过来，三边符合这个规律的，是否就是直角三角形呢？

他搜集了诸多例子，这些事例最终都对那两个问题给予了肯定的答复，他兴奋到了极点，宰杀了一百头牛用以庆贺。

以后，西方人就将这个定理称为毕达哥拉斯定理

参考资料

江晓原，其作品为《周髀算经》新论·译注，出版地是上海kaiyun官方网站登录入口，由上海交通大学出版社出版，时间为2015年06月