牛顿第二定律的应用高一物理课件
这个课件是关于高中物理牛顿第二定律应用的资料，内容主要围绕牛顿第二定律展开，适合高一学生使用，可以用来辅助学习相关知识。这个课件可以直接下载使用，无需进行任何注册步骤，而且是完全免费的，任何人均可获取。牛顿第二定律应用涉及高一物理教学，沪科版高一物理相关内容，文件体积为16KB，资料格式为PPTkaiyun....
生活应用 第111页
初中物理牛顿第二定律适用范围考点
牛顿第二定律主要针对普通物体和较慢速度的运动情形，同样适用于惯性坐标系。这个定律说明，物体加速的快慢程度，同它的重量成反比，跟它承受的总外力成正比。它是经典力学体系里的关键条款，也被看作物理学里的基础准则之一。必须留意的是，一旦物体承受了不平衡的力，它的运动情形就会产生变化，但此时这个定律依然有效。此外，物体...
统计学“凉方”：降降你的认知“暑气”
原创 浙江省统计局 浙江统计 浙江
大清早
妈妈就给小统转发了n条“养生消息”：
中国移动
6:21
妈妈
震惊！张大爷每天一杯芹菜汁，一个月后高血压不药而愈！
震撼研究！七名受试者持续食用黑芝麻三十日，高达八成灰白头发竟恢复为黑色！传说中的养发古方终于得到科学验证！
注意！近期调查表明：常饮XX绿茶者得肝炎...
【趣味统计】生活中无处不在的统计学
研究者无法脱离数据分析而探索，治理者无法忽视数据统计而管理，经营者无法摒弃数据核算而运作。
日常生活中，人们购物时会广泛搜集信息，进行多家比较；在家庭财务规划时，会系统收集数据，权衡不同收益；工作中，对学习成果进行归纳，通过对比来深入分析......即便是日常娱乐时制定各种游戏规则，也离不开统计学的应...
统计学科：大有用武之地
二零一一年二月，国务院学位委员会第二十八次会议审议通过了新版《学位授予和人才培养学科目录》，统计学晋升为一级学科，归入理学门类之下，能够授予理学学位kaiyun.ccm，也能授予经济学学位。这一决定符合时代进步趋势，为我国统计学未来的深入发展创造了更广阔空间。
什么是统计学
统计学探究如何高效地汇集、归类和解...
2015辽宁教师资格中学心理学复习资料:4.2知觉
三、知觉的特性
(一)选择性
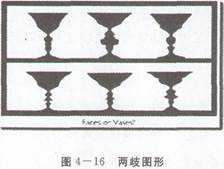
人的周围境况纷繁复杂，不可能在刹那间把握所有事物，总是挑选某个事物作为注意焦点，其余的则沦为衬托kaiyun全站网页版登录，这就是注意力的选择性作用。被注意的事物会变得格外清晰，而作为参照的背景则相对模糊不清。在学习期间，如果人们专注观察黑板上所写的文字，那么这些文字便是他们感知...
浙江宣传 | “身边统计学”靠谱吗
近来，许多网友频繁提及“身边统计学”，借助身边事例来揭示社会状况，诸如“我有个熟人”“我一位同学讲过”之类的表述，已成为网络流行语。
统计学作为一门学科，近代才逐渐系统化，但统计方法、实践及理念在中国源远流长，最早可上溯到原始社会的结绳记事方式。如今大家谈论的“身边统计学”，通常是指部分网友以个人社交圈为参照...
十个例子，教你用统计学方法高效完成机器学习项目
雷锋网报道：该文系 AI 研习社翻译的技术文章，原标题为《10个运用统计方法于机器学习项目的范例》，作者是 Jason Brownlee。
翻译由赵若伽承担，校对工作由陈涛负责，整理事务交由陈涛处理，项目最终由MY监督完成。
统计学和机器学习是两个联系特别紧密的领域。
事实上，这两者之间的分界线时常难以区分。...
心理学：从这张图里你能看到的是姑娘还是老妇？你对知觉了解多少
探心社
每日为你提供心理相关趣闻，助你心情愉悦；呈现心灵探索内容，迎合你的求知欲；深入解读生活困扰，为你消除烦恼。
假如一张类似的照片忽然映入视野，接着询问你，你最先注意到的是谁？是位成年人？是一位年长的女性还是年轻的女性？你是否会因此感到一时语塞？是能够立刻给出回答，还是必须仔细端详一番，才能说出对方是…...