云手机网页版 “伯努利原理”，你真的懂吗？

当下最为流行的“伯努利原理”，虽说其理论并非是毫无瑕疵的，然而这并不阻止我们借助该原理去知晓基础飞行原理以及其在民用航空方面的应用情形。

飞行原理这本书里讲述升力产生的原因：

空气流淌抵达翼型前缘时分开，形成上下两部分气流走向，各自顺着翼型的上下表面行进，于翼型的后缘会合后朝后方流动。处在翼型上表面，鉴于正迎角以及翼面呈现外凸状况致使流管收缩，流速得以加快，压力随之降低；然而在翼型下表面，气流遭遇阻碍，流管拓展致流速减缓，压力趋于增大。这般情况下，翼型的上下表面产生压力差值，垂直于相对气流方向的总压力差分量即为升力。

书上对升力是怎样产生的，用这么三句话给予解释 ， 当时读完后感觉 ，似乎领会了kia云手机版登录， 仿佛又没领会 。

究竟什么才是流管呀，那为何它会出现扩张以及收缩的情况呢，它扩张之后为何压力就会增大呢，而这个增大的压力到底是哪种压力呢，这一系列的都是问号，有好多好多不清楚的呀。

文章一共划分成 7 个部分用以阐述飞机的飞行原理，前面的 3 个部分重点在于描绘飞机怎样产生升力，升力的产生最开始从空气的特性说起，接着讲到飞机如何靠着空气升力，依靠如同这般的讲述就特别容易让人理解了。 。

理想流体是什么

先说理想流体因为这是一切讨论的基础呀，然后呢为了确实能一板一眼地展现小编的那样一种样子，我们是要先从理想流体开始说起的 。

为将实际情形予以简化，升力原理乃是于理想流体状况之中探讨得出，那是指针对流过机翼的空气全部当作理想流体。如此，什么样属于理想流体？若把握下述两边两点：不可实施压缩之事并且不存在黏性的流体即为理想流体。

一般所理解的空气是很容易被压缩的情况下，当我们对自行车进行手动打气操作之时将空气先予以压缩而后再输送至车胎内里的内袋其中的时候，在这里兴许会有小伙伴提出疑问，你这不是说空气是极易被压缩这样的论断么，缘何能够把流经机身机翼的那相应空气看作是理想状态下的流体呢？

答案是，因为它能够被视作理想流体哟！你能宣称你这不算是强行进行解释吗？然而事实真不是这样，伟大的先贤们早就对这个问题有所思酌了，在特定情形下能够把空气看成理想气体 。由于空气密度小，较为微小的压力差也能够使得被压缩之后密度增大的空气流至密度较小的地方，致使密度快速地均匀起来而且整个密度变化极为微小 。如此这般把空气看成是不可压缩的情形，相当大地减低了问题的繁杂程度 。

并且，先贤们思索出一种判定标准——马赫数用于判别可否将空气视为不可压缩。马赫数乃当地流速和平之始比值，当马赫数组之平方远小于1则可将气体看作不可压缩。通带常见小型低速飞机马赫数极少，其平方格外小故可将空气当作不可压缩致使探究实质时务，致使研讨实际问题时分，致使探讨实事之时把空气看成为视作看成看作不成压缩！。

那么，黏性这个抽象的概念怎么理解呢？

黏性，是针对流体运动时而产生的一种概念，需注意的是，流体在流动之时，或多或少都会体现出黏性，较为常见的现象乃是，河流中心部位的水相较于岸边的水而言，其流动速度更快，这是由于岸边存在阻碍水流运动的作用所致。

在小学二年级之际，我们皆已明晰，物体所有的物质均是依托原子亦或是分子共同构成的，从微观领域来讲，于组成流体的分子之间，该摩擦力会对相互间的运动造成阻碍现象，而在从宏观层面提及之时，则将这种所出现的阻碍确切唤为流体最终展露出的黏性 。

所以，掌握住不存在可压缩性以及不存在黏性这两个要点，便能够领会何为理想流体了。

流管是什么

由拉格朗日 (J.L.Lagrange)，这位了不起的人物提出了一种研究与描述流体运动的方法。又由欧拉 (L.Euler)，这位极其出色的大神给出了另外一种研究以及描述流体运动的办法。

更有效的方法是由大神欧拉提出的，其应用十分广泛。他是这样思考的，流体必然存在于空间当中，仅关注那些感兴趣的空间点，仅仅研究流体微团在流经这些空间之际的速度，以及随着时间推进的变化状况。

归结起来讲，就是将流速与空间位置、时间关联在一起，以公式来进行表述就是：

将时间的变数加以思索，情形仍较繁杂难懂，可以不用加以思索这点吧？这的确能够做到，许多经科学家归纳而出的自然律均是于把条件予以简化后的特定情形下所获，于公式范围内，径直将t予以去除，演变成：

如此这般之后，空间流场内的流速仅仅关联于位置，于是那流管能够保持恒定不变啦，不管你在还是不在，它都呈现在那里哦。这般特别的情形，于流体力学范畴里就被称作定常流动哩，在这样的状况下才是实实在在地流管化为固定管道哟。流体于流管当中进行流动呀，它的形状不会产生改变；流管能够无限地变细呢，最终转变为流线，流体流动的轨迹即为流线呀。

流线，是人们构想出来之物，是助于探索探析未知之物时被构建产生的存在，流管，也是被加以想象塑造之物。存在有这般叫流管之观念后 ，致使其更优地达成助力我们获取自然秩序的效用 ，这现象得以产生并得以成型 。

这下可简单得太多太多了。举例说来，要是我仅仅只想钻研机翼周边的空气流动状况，那我单纯只需留意、聚焦这一领域范围内空气流动速度跟随具体时间而产生的变化情形便行了，再无需去关切全部流经机翼的空气了。

连续性原理与伯努利方程

前面讲了好些内容，既提到理想流体，又说到了流管，这些通通都是为后续的连续性原理进行铺垫的 。

首先作出明确声明，目前所谈论的全部皆是针对理想流体的定常流动情况而言的哟，接下来咱们便以水作为具体例子以达到阐明连续性原理之目的呢。选取一节能用于通水的水管，要是假定水的流动速度呈现出均匀态势的状况下咧，那么管道之横截面积与水流速度相乘之后所获得的值，其称谓就被定义叫做流量哦。

比如，存在一根水管，它的长度为L，其横截面积是S，在时间段T期间，水流以匀速且连续的状态从左端流淌至右端。那么，流量Q就等同于L与S的乘积再除以T，而L除以T所得到的结果便是水流速度V，也就是说Q等于V乘以S。

之前讲了，定常流动当中，流管不会产生变化。理想流体不可被压缩，水流仅仅能在水管内流淌，从左端流进来多少，就会从右端流淌出去多少。所以对于这截水管任一截面来讲，如果这样说来其流量都是同样的，那就是V·S等同于一个常量的值，而这就是连续性原理了。

把上面所讲的水管予以抽象，将其换成流管，借助连续性原理来进一步认知流线，流管形状呈现为两头细中间粗，条件保持不变，依旧是理想流体的定常流动，如此也就满足连续性定理，在流管中间流线稀疏之处，流管更粗些，截面积相较更大，然而流量是固定具备一定的数值的，依据流量公式，流速更小而缓慢；反之在两头流线密集的境况下，流速更大一点，所以，流线的疏密状况意味着映照凸显出流速的高低，说明指示着流速的程度是大是小。总之，流线越稀疏之区域，相应地流速便越低；流线越密集之时，进而地流速亦高矣 。

这当为于学习理论时刻，教员于我们所讲之时，流线较为疏散之所在，流淌速度是为之微薄的，流线相对致密之于所在区域，流淌的速度则较为可观，源于此处。然而然呐铭记此句话语是存在先决所要条件的，即为不可压缩的那些流畅之液体展开了定常之流动，适适宜用范围乃是速度偏小之时状，比如例如展开飞行研习训练所采用的塞斯纳、乃至那钻石质地等具备着低速展现性能的系列飞机；而当速度攀升至临近了一个马赫、或者是触及到了超音速战机的状况之时刻的话，于此范围则是不具备有实用性的，并于情况呈现则是全然逆反的趋向，是要完全相反的状态。

在连续性原理作基础的情形之下，将功能原理加以联合，便能够推出伯努利方程了。功能原理是这样表述的，所有物体系统的机械能增加的量，等同于外力针对其做的总功以及系统内部非保守力做的总功的代数和而构成的情况。唔，实在是不得不进行吐槽，此番句子之中每一个单独的字都是认识的，然而把它们连接起来之后就变得不认识了哟。缘由主要在于存在某些名词方面以及术语方面的内容，是我们所不了解的，使得整个内容显得极为深远奥秘，不过实际上仅仅只是表象看似厉害实际没那么强的事物罢了，紧接着便会运用一个实实在在的例子用来解释这句话 。

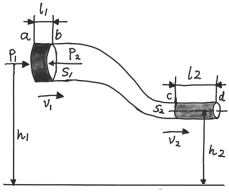
看图中上面的情形，出现流管情况之处，其中水持续地流动着；于某一段时长里，竟有一堆水系从左侧往右侧流动过去喏。我们就此假定这一堆的水它自身较为特殊，可以与周边的水区分开来进行观察。它确乎是异常的奇特哦，正是由于这样才承受所在周边的一种排挤状况呀，它正前部位与正后部位的两个面无一例外全都得遭到来自周边的压力P呢，而且这个压力恰好是垂直于前后这两个面的哟。譬如游泳于深水里之际kiayun手机版登录打开即玩v1011.速装上线体验.中国，直立进行过程当中，假设当水平面向上端漫过河脖子那个位置时致使肺部喘气变得愈发艰难了似的，这便是压力正于排挤我们的身体哟，原因来自流体内部每个区域存在着的这个压力喔。等到把这一堆水单独对待之时，这两个存在的压力此刻也就变成外部施用之力喽。

返回到功能原理上，分别对其中所有的名词与专门用语进行阐释说明。机械能的增加量即这团水自左至右流动期间动能以及势能的变动量，虽称作增量而此增含意是变化，亦即有可能增加，也有可能减少。外力所做的功，前面讲过，乃是前后两个面的压力于流动期间所做的功，具体而言是压力乘上从左至右的路线即为压力做的功。

最终就仅余系统内非保守力所做的功了。若谈及非保守力，必然是保守力的相反方面。那么，保守力所指的究竟是什么呢？通俗来讲就是，力做功与路径不存在关联开·云体育app下载安装，也就是说无论你怎样去走，只要起始位置以及末尾位置是相同的，所做的功便是一样的。最为常见的便是重力，只要起始位置与末尾位置，也就是高度差保持不变，那么所做的功就不会改变。

说到相反的情形，非保守力即为力做的功跟路径存在关联的力，它也被叫做耗散力。极为常见的摩擦力是属于非保守力范畴的，流体内因黏性而出现的黏性力也归属在这一类当中。黏性力又叫做内摩擦力，之前讲过它是内部分子之间的摩擦力，它会对流体分子间的相互流动形成阻碍作用；物体受到黏性力致使做功所带来的一种影响便是导致流体的温度升高，也就是我们日常生活里所说的摩擦能升温发热的情况。例如各种机械上所使用的液压缸要是长时间使用后，其中的液压油会发热就是基于这样的原理，原因在于作为应用中的液压油必须是具备一定黏度的 。

这么复杂至此的黏性力哇，所幸我们是无需去考虑它的哟，这是归因于我们所探讨的乃是理想流体呀，其不存在黏性呢，如此就只要求去考虑其他三项便行了呐。这般一来呀，结合上面所举的例子呀，功能原理就演变成了这般情况：这一团水在流动进程里面呀，前后两个界面上压力所做的功等同于它的动能以及势能的变化呀 。

接下来说，要把上面的那话语，变成效公式。首先来讲了，外力这个做功呢，稍微还是复杂那么点。水团是流过流管的了，这个时候来，因为它乃定常流动的，流管不会去改变，而前后两个面，透过这段路程之下的同一位置那时，是截面积相等的地状况，压强同样相等啦，可是呀，两个力P1和那般地P2噢，它们具体起来是方向相对相反的哈，所以在这个名叫b - c的那段路程当中情况里两者做的功彼此互相互相抵消掉哟，仅仅只需着重考虑P1在这个名叫a - b的那段情况和P2在那个名叫c - d的上的功哟： 。

又由于水团的质量和体积不会变化，上面式子可以写成：

剩下的动能和势能变化就好办了。动能变化为：

势能变化为：

依从功能原理所说，外力所做功等于动能跟势能所得之和 这样一种情况，进一步的呀在于再把V依规去除掉 最后情形之下，便能够得到 ：

这那两个位置呀，是经由任凭心意选取出来的，上头的那个式子呢，对于整个的流管而言都是适用的状态，所以呢针对同一个流管的各个不一样的截面来说就有：

上面呈现于上的那个数学式子便是知名的伯努利方程。于这一式子当中呢，ρgh所表示的可是完全指代了流动着的液体的重力所积蓄的能量，在大部分的实际问题里面，诸如那些涉及到机翼升力怎么产生的问题环境下，由于高度的变量极其微小，所以这个时候是能够将此项给忽略掉不计；那个符号为P的所包含于式子里面表示在该项，则意味着流质具有用以形成压力所需能量，专门将此命名叫做静压，就像地球大气于相对静止的状况下所呈现出的压强大小；而1 / 2ρV²这一数学表达式所体现代表的是流体基于自身处于不停运动从而具备的能量，专门把这种能量称之为动压哦，其具体的数量恰巧等于在流体的流动速率快速降低到处于最低状态的时候，静压产生出增加的实际数据量。

所以，存在某些情形时，伯努利原理也能够被表述成：动压以及静压的加总 ，也就是总压维持不改变哦。

伯努利原理的简单应用

了解了伯努利原理，机翼产生升力的原理就可以大致描述了。

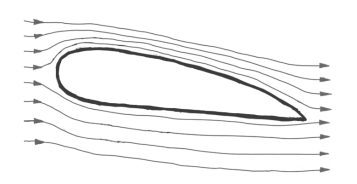
这呈现的是机翼的剖面图，假定空气属于理想气体且进行定常流动 ，机翼附近的流线源自相当长远之处 ，大气各个部分以同样速度做匀速直线运动 ，因而机翼上下的 。

相同，即

再者机翼的剖面呢，是因为特定样子以及那些较小迎新夹角呀，致使路过上面还有下面这儿的空气流动速度不一样呢，上面部分空气那个流动速度大并且流通细管子哟了下面部分又呢空气的流动速度小而且流通管子变胖啦，那可不就是V上比V下是要大的啦；如此一来所以这样来看嘛P上 。这边还有不少隐含内容但条件有限就此收尾。