kiayun手机版登录app游戏登录入口.手机端安装.cc 【AI系统】卷积操作原理

卷积，属于神经网络里的核心计算当中的一个，它是一种特别的线性运算，卷积神经网络也就是 CNN，是针对图像领域任务所提出的神经网络，其受到猫的视觉系统启发，通过堆叠使用卷积层以及池化层来提取特征，它在 CV 领域方面取得的突破性进展引领了深度学习的热潮。

转回卷积自身，它的变种繁杂多样，计算过程复杂，神经网络运行期间大部分时间都花费在了计算卷积上，神经网络模型在持续进展，其发展过程中不断加大网络的深度，所以对卷积计算予以优化就显得格外重要 。

本文会先介绍卷积于数学范畴里的定义，借助信号处理领域的一个实例去阐明卷积的过程，随后给大家介绍CNN里卷积计算的有关知识，在知晓卷积计算的前提之下，本文会接着给大家介绍卷积于内存中的数据格式以及张量里的卷积计算过程。

卷积的数学原理

在通常形式里，卷积属于一种数学运算，它针对两个实变函数。在泛函分析范畴内，卷积也叫旋积或者褶积，也就是Convolution，这是通过两个函数f以及g来生成第三个函数的一种数学运算，其本质是一种特殊的积分变换，是对函数f与g经过翻转和平移后的重叠部分函数值乘积针对重叠长度的积分。

卷积神经网络又称Convolution Neural Networks，别名叫做CNN，其概念是从信号处理领域的卷积拓展而来的，信号处理的卷积有着这样的定义，那就是：

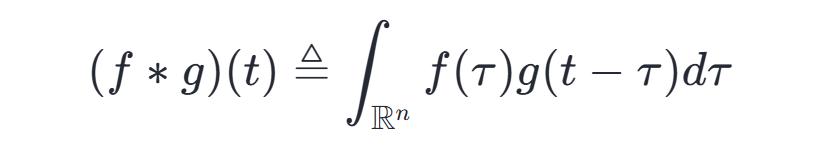
能予以证明，针对于近乎所有的实数x，伴随x的各异取值，积分界定出一个全新函数h(x)，此函数被称作函数f与g的卷积，记作：

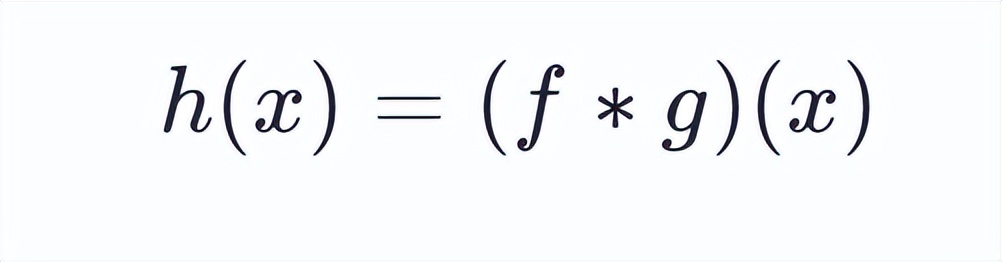
对于信号处理的卷积，其定义是连续的表示，实际计算时，会将连续的形式，采用离散的方式来进行计算：

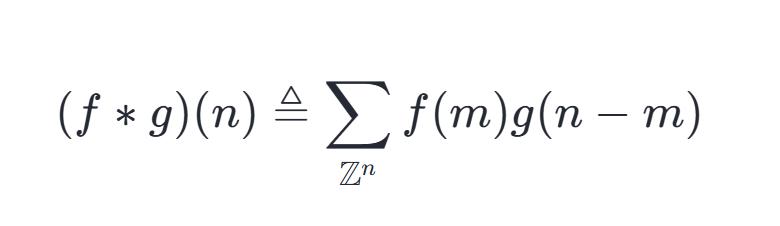
通俗定义

对于卷积计算而言，从直觉方面来讲不容易被理解，其经过可视化之后如同下面所展示的图形。在图中，红色的滑块处于移动进程里，它与蓝色方块的乘积被绘制而成的三角形状图案，就是卷积结果在各个点上所对应的取值：

更具体来说，解释卷积需要清楚“卷”和“积”两个步骤。

“卷”的过程

根据上述介绍中卷积的定义：

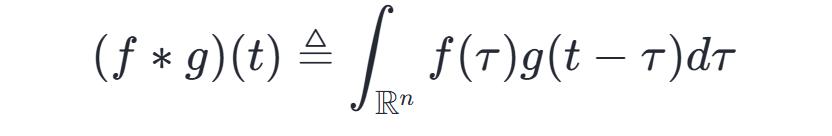
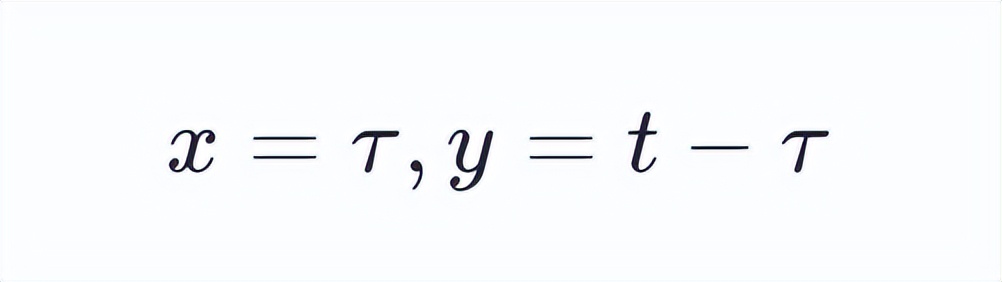
则有 x+y=t 成立。

也就是说，处于卷积进行时，函数f(x)里x的取值，以及函数g(y)中y的取值，会受到线性函数x+y=t的限制。要是让t等于10，那么x,y的取值序列就有着如同下面所展示图形那样的对应关系。从直观角度来讲，x,y的取值存在一种呈现翻转对应的感受。

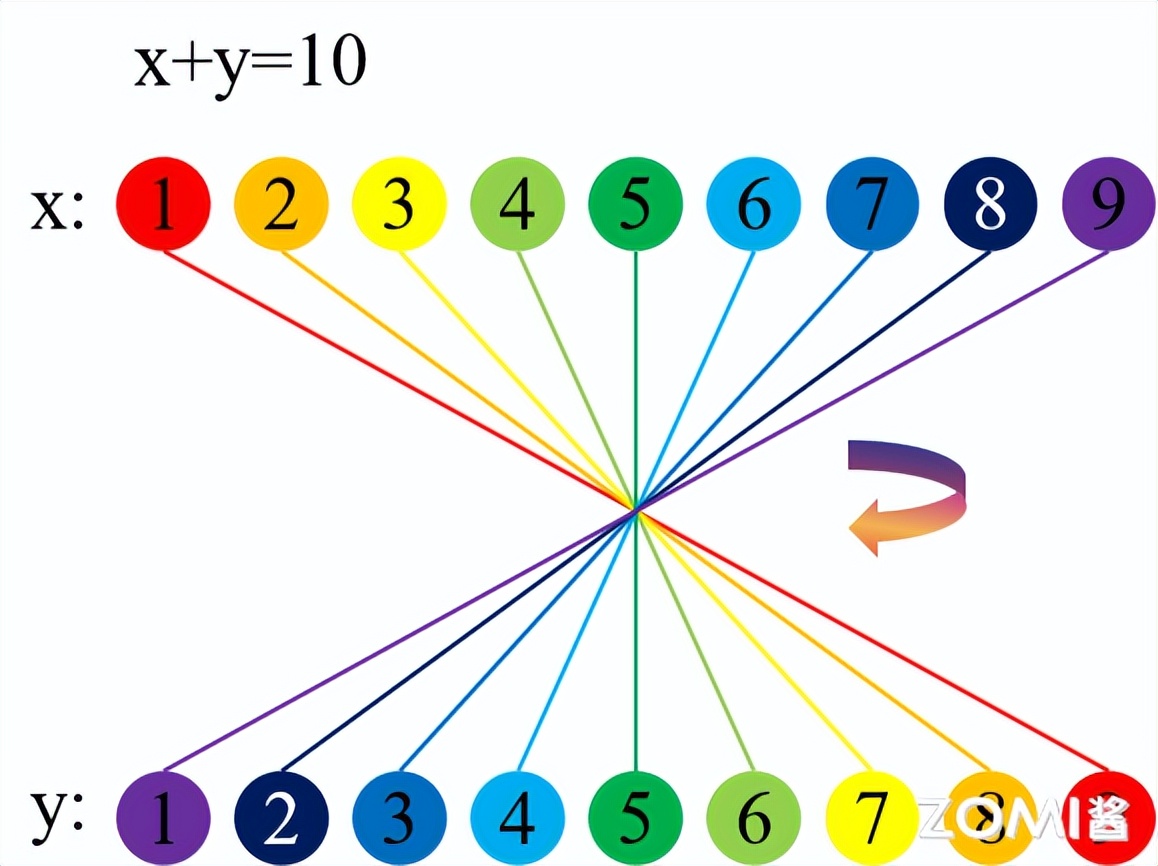
2. “积”的过程

t 的取值发生变化时，x 的取值被约束在，斜率为 -1 的直线簇中，y 的取值同样被约束在，斜率为 -1 的直线簇中。

定义：

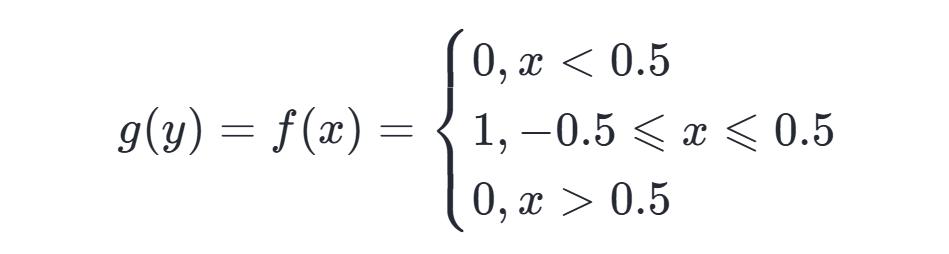
在下图（左）里，t 的取值呈现出这样的情况，从上到下依次是 -1云手机网页版，-0.5，0，0.5，1 ，令 y 等于 t 减去 τ ，x 等于 τ ，左图之中有着红线，它是 g(t 减去 τ) 的函数图像，同时还有蓝线，它是 f(τ) 的函数图像。存在黄色区域，它属于不同 t 的取值条件下参与卷积的有效区间，另外有着黑色直线，其最右端的点的取值就是卷积结果。

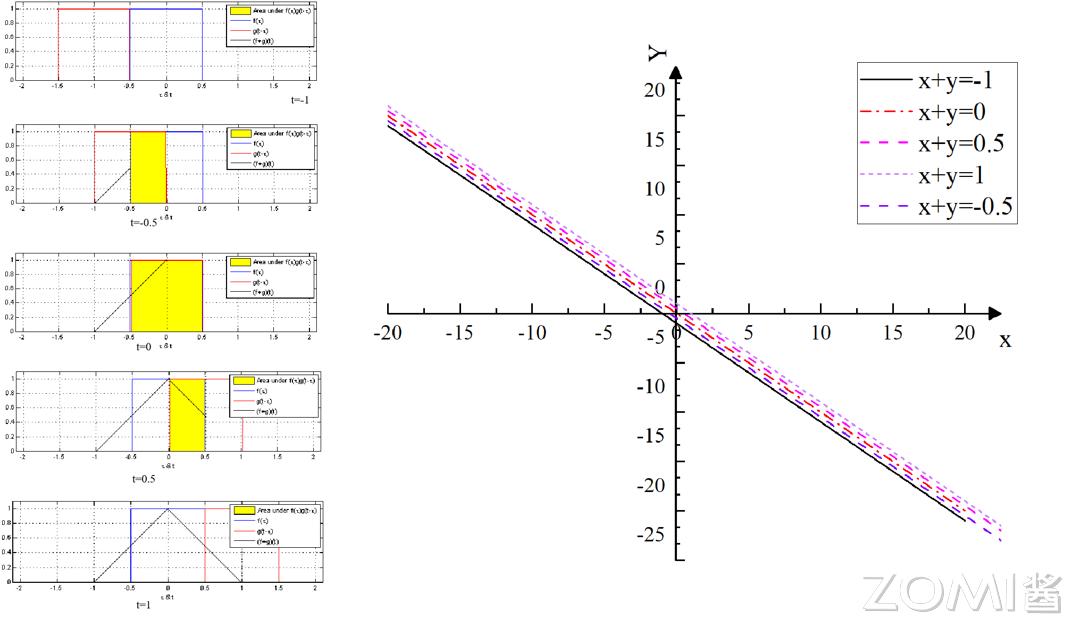
总共概括来讲，积分其本质是能够被理解成求和的极限，卷积之中“积”的进程实际上是相互对应的函数相乘以及求取积分的进程。

具体例子

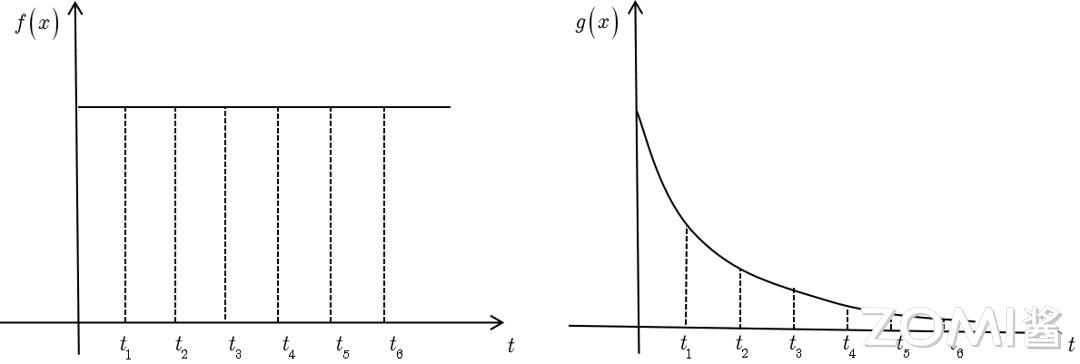
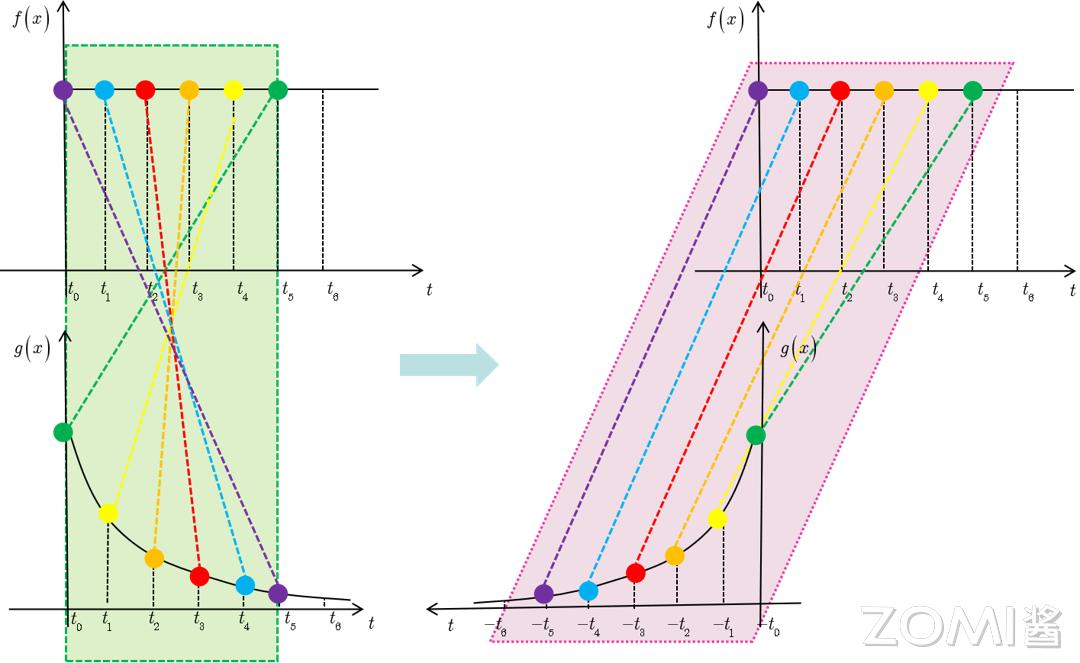
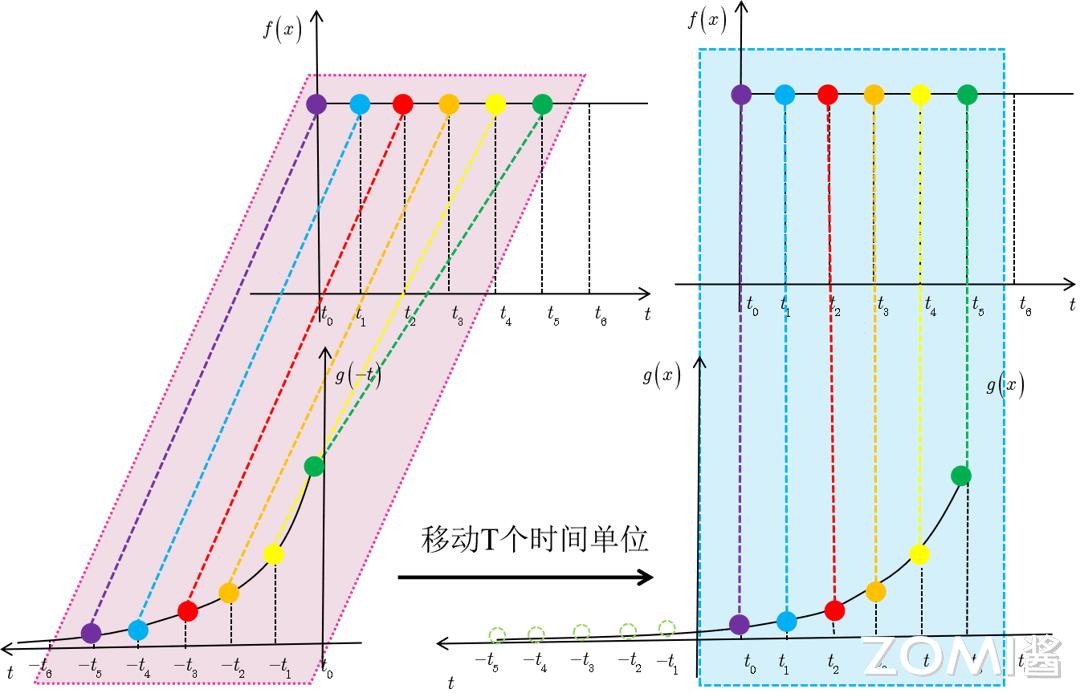
以信号处理的系统响应函数为例：

定义，输入信号为 f(t)，它随时间变化，但其数值保持不变，系统响应函数是 g(t)，图中的响应函数随时间指数下降，它的物理意义为，如果在 t=t1 的时刻存在一个输入，那么随着时间的消逝，这个输入会持续衰减。

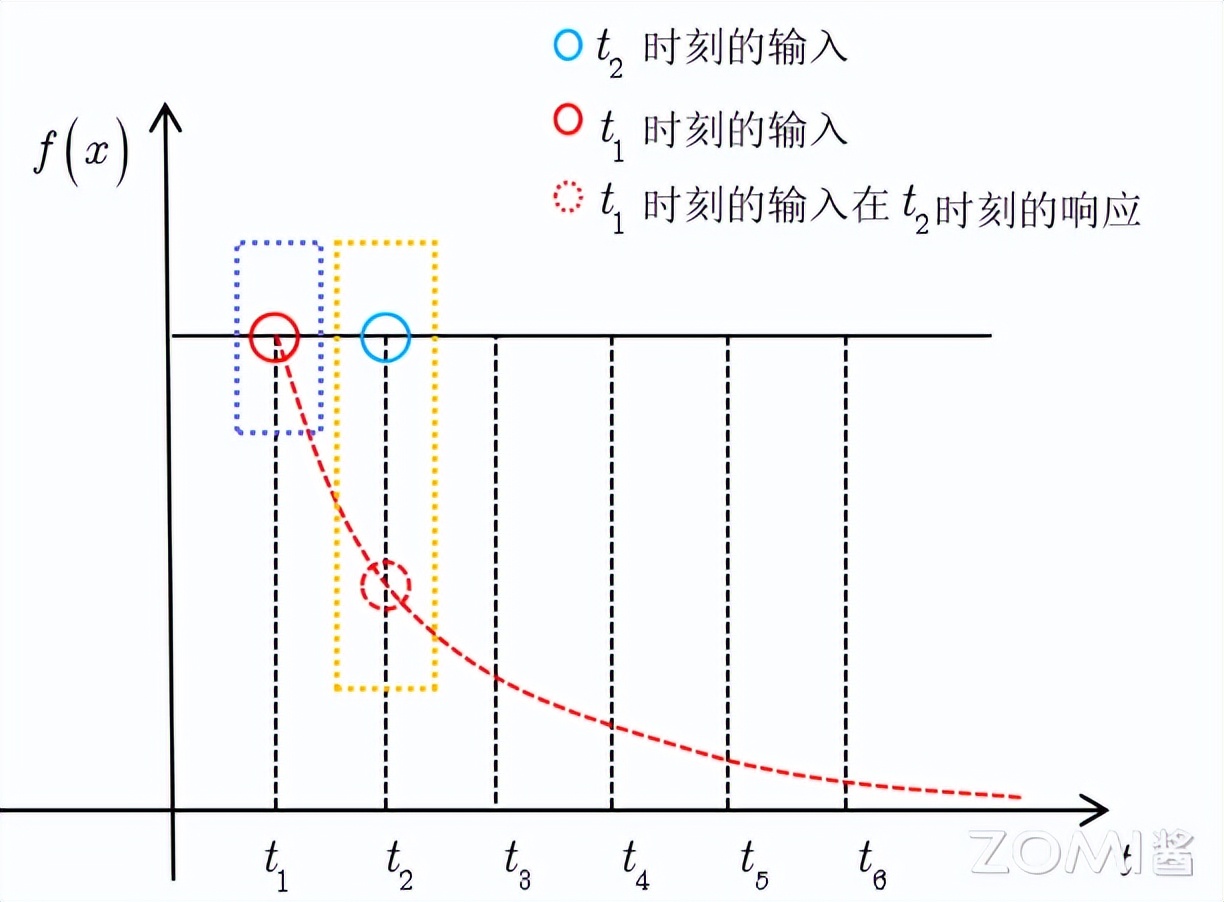
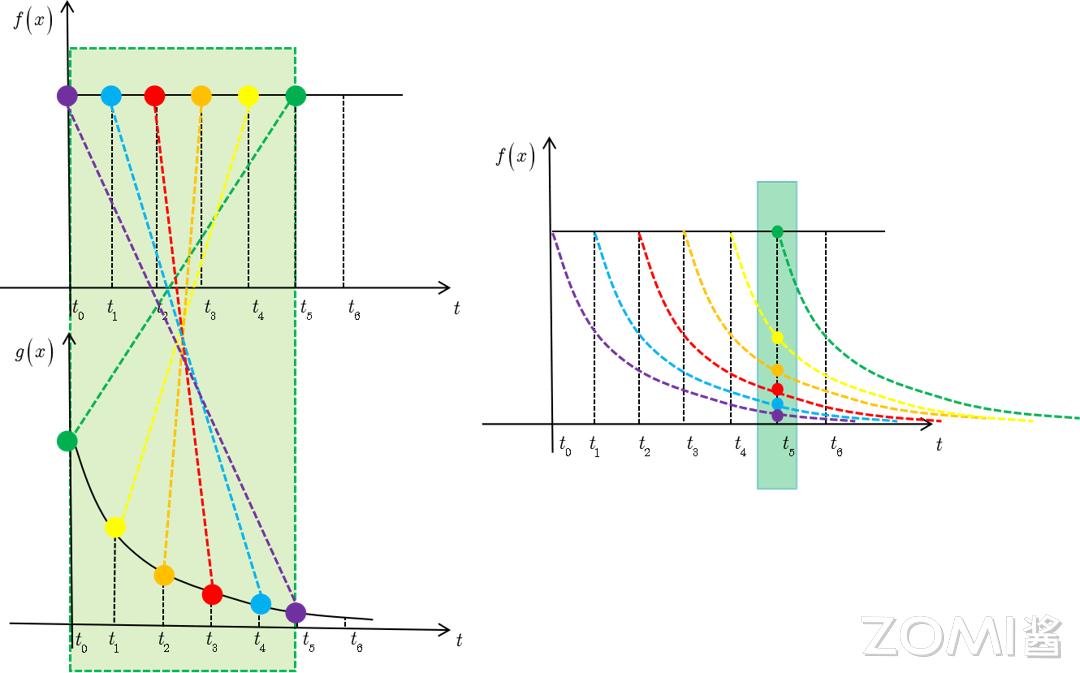
卷积的性质

卷积满足以下的数学定律和具体的性质：

交换律是， f 与 g 进行 ∗ 运算的结果等于 g 与 f 进行 ∗ 运算的结果，即 f∗g=g∗f ；结合律是，先对 f 与 g 进行 ∗ 运算，所得结果再与 h 进行 ∗ 运算，等于先对 g 与 h 进行 ∗ 运算，所得结果再与 f 进行 ∗ 运算，也就是 (f∗g)∗h=f∗(g∗h) ；分配律是，f 与 g 加上 h 的和进行 ∗ 运算，等于 f 与 g 进行 ∗ 运算的结果加上 f 与 h 进行 ∗ 运算的结果，即 f∗(g+h)=f∗g+f∗h ；单位响应是，存在一个函数 δ ，使得 f 与 δ 进行 * 运算的结果等于 f ，也就是 f∗δ=f 。

其中，δ是狄拉克δ函数，此函数为连续的，或者，δ是单位脉冲函数，该函数是离散的 。

卷积物理意义

卷积的物理意义，由它所应用的具体领域来决定。在不同领域里，卷积能够表示不同的物理过程。

信号处理

在信号处理领域之中，卷积的物理意义一般是关乎系统的响应的，假定我们存在一个输入信号 f(t) ，像比如说一个音频信号，并且设有一个系统针对该信号的响应 g(t) 也就是系统的输出，系统的响应 g(t) 能够是理想状态的，也能够是通过实际测量而获取到的 。

当输入信号f(t)经由系统时，系统有能通过卷积f∗g进行计算的输出h(t)，这里的卷积意味着系统针对输入信号做出的累积响应，详细来讲，h(t)于任意时刻t的数值是输入信号f(t)同系统响应g(t)在往昔所有时刻的加权叠加，权重由系统响应g予以确定，这体现系统对不同时刻输入信号的“记忆” 。

比如说，要是存在一个系统，其对于输入信号的响应会呈现出滞后的情况，那么输出信号h(t)就将会是输入信号f(t)的一个平滑版本，在此其中，g(t)对平滑的程度具有决定性作用。

2. 图像处理

在图像处理里头，卷积常常被用于滤波以及特征提取，于这般情况下，图像能够被视作二维信号 f(x,y) ，在这里面，f(x,y) 跟 y分别是图像的水平坐标与垂直坐标，卷积核 g(x,y) 是一个小的权重矩阵，它在图像之上滑动，去计算每个像素点的加权平均值。

这个过程，其物理意义在于，把图像的每个像素点，同其周围的像素点，予以比较开·云app体育登录入口，借由加权平均，去确定此像素点的新值。卷积核g的设计，决定了这般比较的方式，举例来说，边缘检测卷积核，会突出显示图像里强度变化颇为明显的区域，由此检测出边缘。

3. 概率论

从概率论方面讲，存在两个独立随机变量，其联合概率密度函数的卷积，给出了二者和的概率密度函数。此背后的物理意义为，设有两个随机过程，它们各自产生随时间变化的概率密度函数，那么这两个过程叠加后新产生的过程的概率密度函数，能够借助对原先的两个概率密度函数进行卷积而获得。

4. 其他物理系统

在别的物理系统内，卷积能够表示扩散进程、波的传播、材料的混合之类，在这些情形下，卷积描绘有关一个随时间以及空间的分布产生变化的物理量（像温度、压力、浓度等），它是经由系统里各个部分之间的相互作用以及传播效应累积所致的。

总的来讲，卷积的物理意义在于，把两个函数或者信号，以一种特定方式进行结合，进而产生一个新的函数，这个新函数在一定意义上，代表着这两个函数彼此间的相互作用或者混合，其具体意义因应用领域以及函数信号的物理含义而有所不同 。

离散卷积

从上文信号分析的部分中，我们得到离散形式的卷积公式：

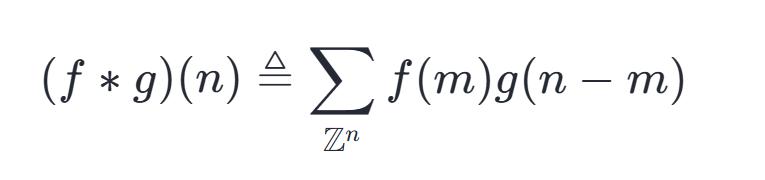
离散序列中的数，存在两个，将其按照规则，两两相乘，之后再相加，这样的操作，被称作为离散卷积。

离散卷积能够被视作矩阵进行乘法运算。然而，该矩阵里头的某些元素被限定为必定要跟另外一些元素保持相等。举例来说，针对单变量的离散卷积而言。矩阵每一行当中的元素，都与上一行对应位置平移一个单位的那些元素是一样的。这样的矩阵被称作Toeplitz矩阵。

把上述离散卷积公式，朝着二维空间去拓展，这样就能得到神经网络当中的卷积，它能够被简写成为：

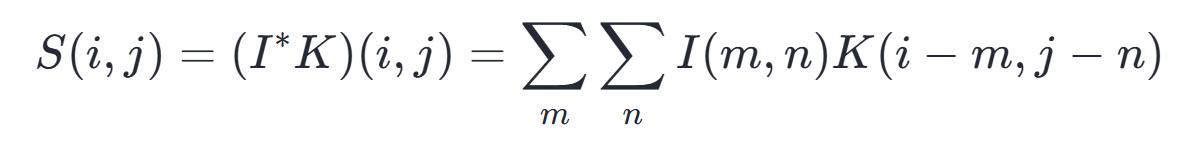
当中：S是卷积的输出结果，I是卷积的输入内容，K是卷积核的尺寸分量。缘由于卷积是具备可交换性质的这 一情况缘故所在我们能够等价地进行写作：

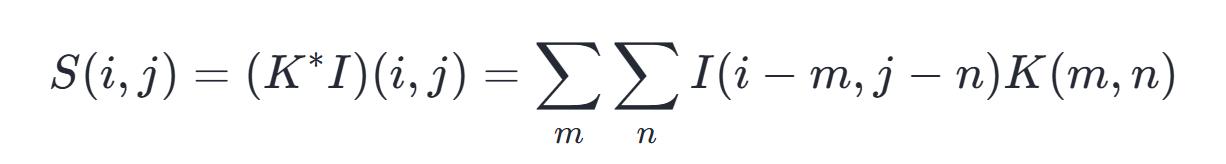
在二维情形下，卷积对应着一个双重分块循环矩阵，除元素需相等的限制外，卷积通常对应着一个极为稀疏的矩阵，这是由于核的大小通常远小于输入图像的大小，无论何种使用矩阵乘法且不依赖矩阵结构特殊性质的神经网络算法，都适用于卷积计算，并且无需对神经网络作大的改动。

在卷积网络有关叫法范畴内，卷积的头一个参数 f 常常被称作输入，第二个参数 g 被称作核工具，那个输出有时被叫做特征映射，于机器学习运用里，输入一般是多维数组构成的数据，而核一般是凭借学习算法优化而得的多维数组的参数，我们将这些多维数组称作张量。由于输入与核里的每一个元素都得明确地分开来存储，我们一般假定在存储了数值的有限点集之外，这些函数的值均为0 ，这表明在实际操作的时候，我们能够借助对有限个数组元素求和来达成无限求和。

CNN 卷积计算

卷积神经网络由三个部分构成，分别是卷积层，池化层，全连接层。卷积层作为其核心部分，通过对输入图像做卷积操作来提取图像特征。卷积层输入通常为多通道的，像多通道图像那样，每个通道代表一个特征，其输出同样是多通道的，每个通道表示一个不同特征。池化层用于降低特征图的空间分辨率，以及增强模型对输入图像的平移不变性跟鲁棒性。用于将卷积和池化层所提取特征进行分类或者回归的通常是全连接层，它的输入是一维向量，其输出维度跟任务的分类数或者回归值的维度并无二致。

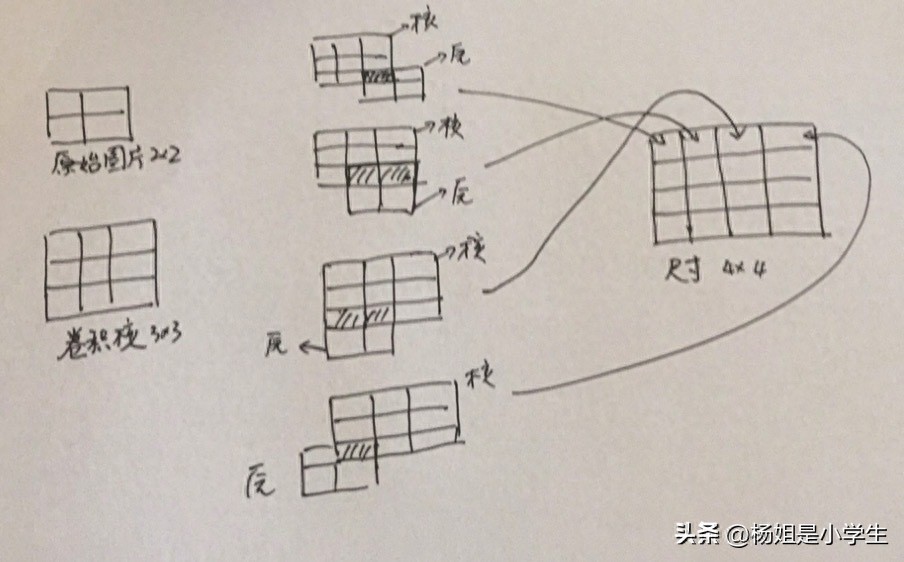
如下面所展示的那样，存在神经网络里边的卷积计算流程，它能够被描述成，一个呈3∗3样式的卷积核，在一幅大小为8∗8的图像之上产生滑动的情况，不管是在哪一次发生滑动的时候，只要把这个卷积核以及处于对应位置那里的众多元素，实施相乘下一步之后再开展求和的操作，其中标记为青色的区域就是它相应的感受野。

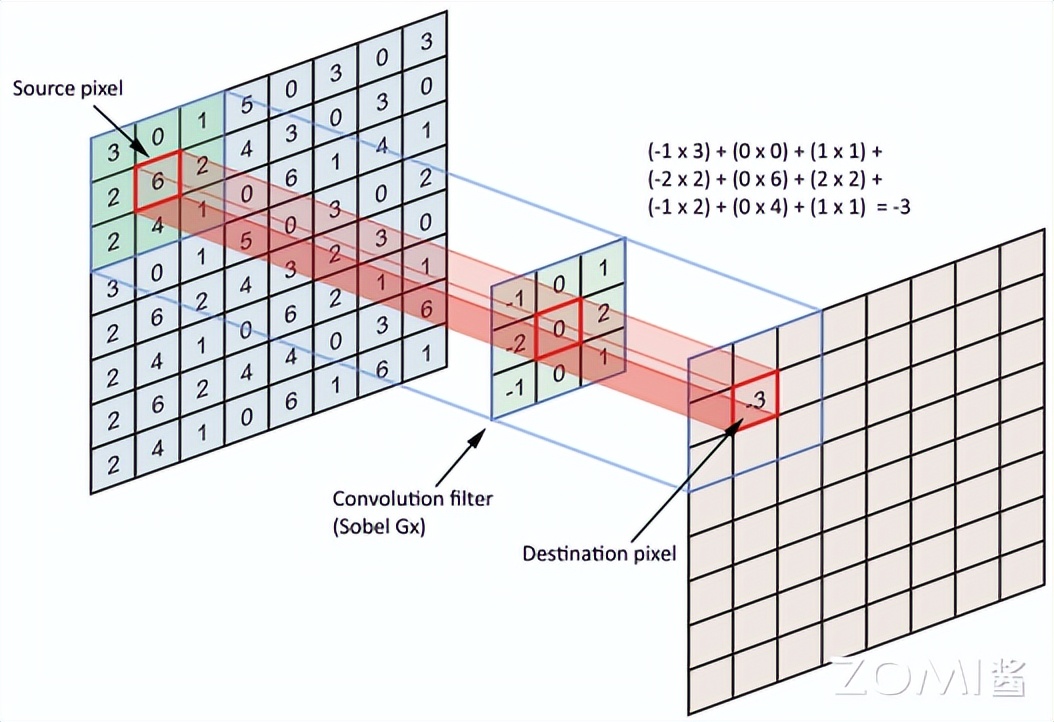
名词解释

在卷积操作的进程当中，会关联到好些专业名词以及各异的计算方式，就比方说Padding、Stride、Channel、Kernel等等，接下来呢，将会深入地去介绍不同名词相互之间所存在的关系以及所展现的表达含义。

保护（Protecting）：避免图像边缘讯息遗失，于输入图像的周边增添额外的行或者列，一般以“0”实施充盈。其用以让卷积之后图像分辨率保持不变，便利计算特征图尺寸的变动，填补边界。

填充背后的数学原理是如此这般，倘若我们存有一个 n×n 的图像，运用 k×k 的卷积核去做卷积，那么输出的大小即为 (n−k+1)×(n−k+1) 而如此一来会存在两个缺点：

针对以上两个问题，我们所采用的方法便为填充，假设填充的行/列数是 p ，鉴于我们在其周围都填充了一个像素点，所以输出就变成了 (n+2p−k+1)×(n+2p−k+1) 。

通常存在 3 种 Padding 的方法，分别为 Valid 方式 ，Same 方式 ，以及自定义 Padding 。

Valid 方式

对于“Valid”而言，其意思是不进行填充，要是这样的情况，当输入是呈现为n×n的图像时，运用k×k的卷积核参与卷积操作，最终将会得到(n−k + 1)×(n−k + 1)的输出结果。

Same 方式

输出大小和输入大小一致被称为 Same 情况发生之时，依据原始的输入来进行计算，所得到的输出尺寸是 n−k+1 ，当填充 p 行或者列之后，公式就变成了 n+2p−k+1 ，让 n+2p−k+1=n ，从而使得输出与输入大小变得一样，求解得出 p=(k−1)/2 ，这样就导致了两种情况的出现开·云体育app下载安装，要是 k 是奇数，能够直接按照公式计算得出 p ，要是 k 是偶数，那么就只能去进行不对称的填充（就像左边填充多些而右边填充少些这种方式呢），以此来确保输出尺寸保持不变 。

自定义方式

意为填充自定义的行，自定义意为填充自定义的数据列数。定义 w 是图的宽，定义 h 是图的高，其生成的特征图大小的计算公式为：

步长，即Stride，它指的是卷积核于每一次卷积操作之际滑动的距离，步长大小是能够对输出数据大小产生影响的，也是能够影响特征提取能力以及计算复杂度的，当步长增大之时，输出数据尺寸会减小，特征提取能力会变弱，不过计算速度会加快。

我们能够将Stride的进程视作针对全卷积函数输出的下采样举动，要是希望于输出里每个方向上隔s个像素开展采样，亦或是在图像之中卷积核的滑动距离成为s，那么这般过程能够借由公式予以描述为：

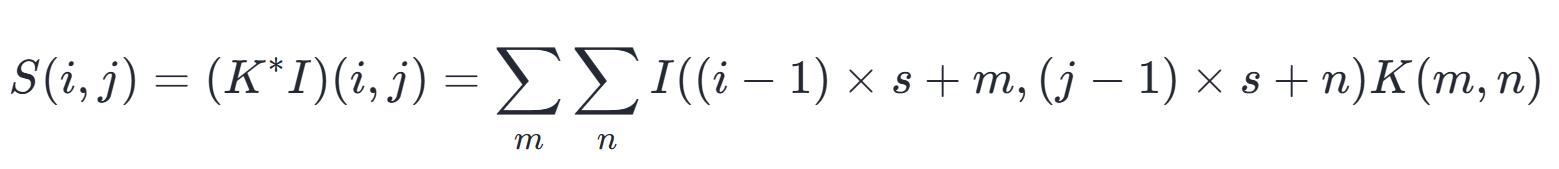
3.通道数，其亦被称作深度或者特征图数量，指的是卷积神经网络里每一层输出的特征图个数，通道数的大小对卷积神经网络的特征提取能力以及计算复杂度有着直接的影响 若增加通道数，能够增强卷积神经网络的特征提取能力，然而也会使计算复杂度增加 。

4. 卷积核（Kernel）：它是算子，这个算子有着可学习的参数，它被用来对输出图像做特征提取，得出的输出一般是特征图。每一个卷积核都代表着一种模式或者特征，存在几个卷积核就会有几张特征图，并且每一个卷积核都对应着一个特征图。在机器学习现象里，卷积核具有的那些参数是依靠反向传播或者梯度下降算法来计算更新的，并非是人工去进行设置。它具备的特点是：1）卷积核每次仅仅连接K×K区域，K×K是卷积核所拥有的尺寸；2）卷积核参数会重复使用（也就是参数共享），在图像之上进行滑动。

朴素卷积过程

将卷积神经网络CNN每层的相关参数进行定义，其目的在于能够以便更好地去理解后续所存在的示例，具体内容为：

H：图片高度 hight；

W：图片宽度 width；

C：原始图片通道数 channel；

N：卷积核个数 Number of Kernel；

K：卷积核高宽大小 Kernel Size；

P：图像边扩充大小 Padding；

S：卷积核窗口滑动的步长 Stride。

首先定义P等于0，接着定义S等于1，然后以N为6个卷积核，作用对象是一张W为5，H为5，C为1的图片，进行卷积的过程所经历的步骤如下：

一个卷积核，覆盖在 K×K = 3×3 的区域，对应位置的数据，先相乘，之后相加，每个卷积核，都针对 1 所述区域，做乘加操作，表示在不同通道，也就是 Channel 对应位置相加在本例中每个卷积核的通道数 C = 1，借此得到的结果，是特征图上相应位置的数值。

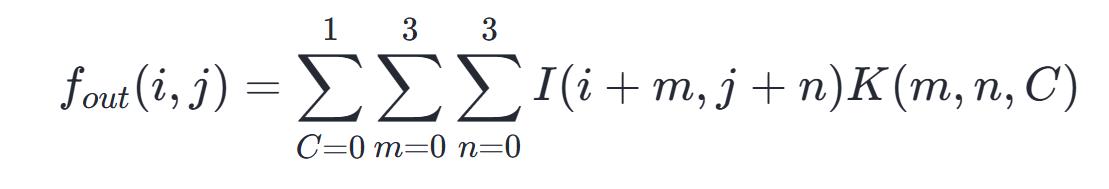
1,2 步骤的过程如下图所示。

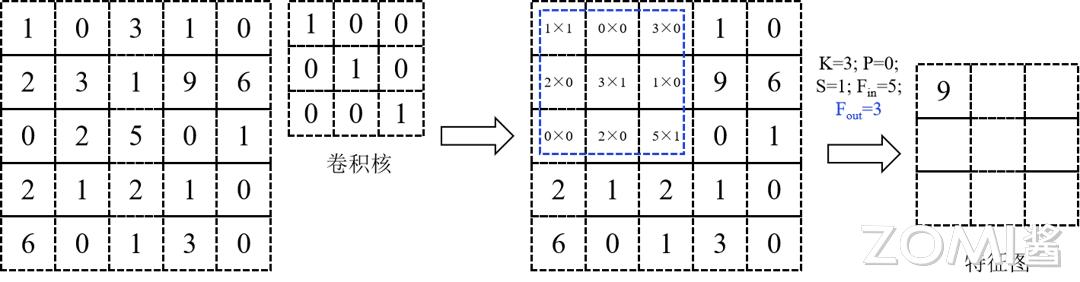
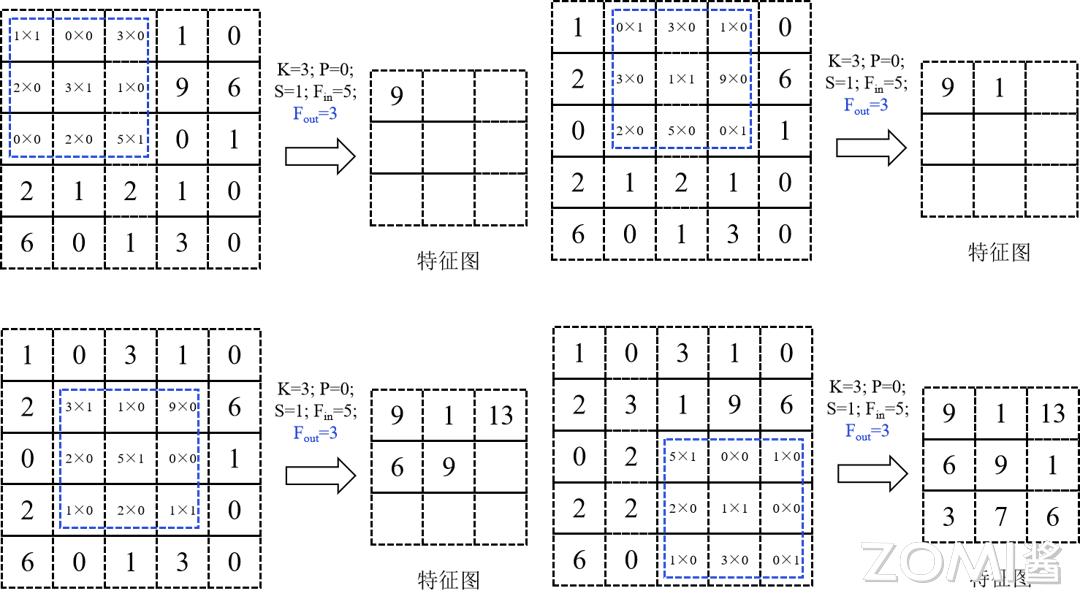
每当进行一次滑动，便会计算得出第l个特征图之上的一个像素点，就如同上面展示的图形那样。而其滑动的总共次数就是特征图的像素点数量。

假设有多个通道，假设通道数量为C且C等于3，那么每个通道中，处于(i.j)位置的值，会对应进行相加操作，从而得到最终结果：

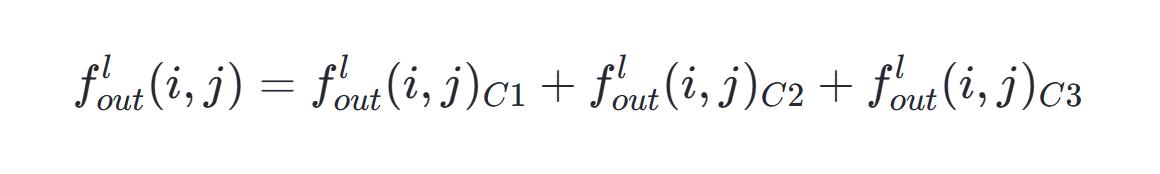
当在卷积神经网络里于层与层之间开展计算之际，发生在1步骤之后，紧接着又在2步骤之后，通常是需要增添偏置量b的，目的在于打破卷积神经网络所具有的平移不变性，进而增强神经网络自身的拟合能力，：

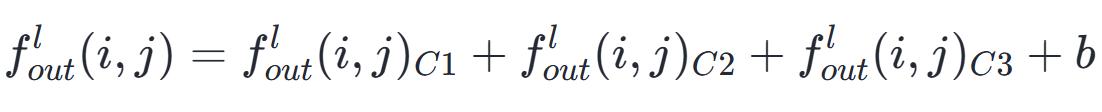
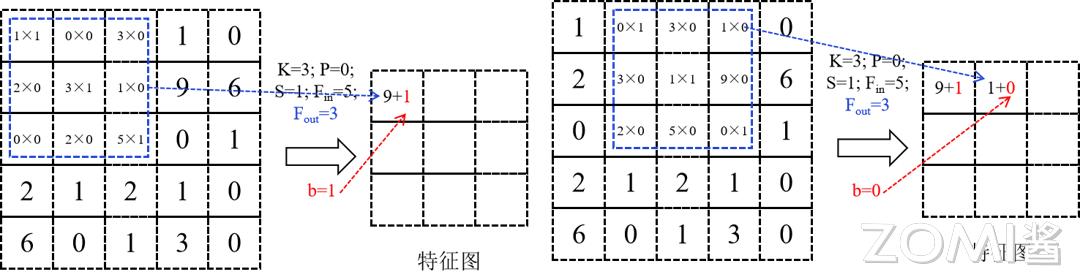
于卷积操作里，卷积核属于可学习的参数，其参数进行更新是由梯度下降算法予以确定，经由上面的介绍，能够知道每层卷积的参数量是C×K×K×N，卷积层的参数数量较少，这同样是由卷积层的局部连接以及共享权重特性所决定的 。

进行局部连接后，每个神经元只是和输入神经元的一块区域相连，这一块局部区域被称作感受野，也就是receptive field。在实行图像卷积操作期间，神经元在空间维度是局部连接，这里的在空间维度指的是在图像平面滑动区域，不过在深度，也就是通道方面的计算上，神经元是全部连接。这样的局部连接使得学习后的卷积核能对局部的输入特征产生最强的响应 。

权重共享，计算同一个输出特征图时所采用的卷积核为共享状态，也就是说当一个卷积核在输入图像上滑动时，会产生一张特征图，该生成的特征图里的每个像素点，皆是由上述卷积核在输入图像上滑动并进行卷积计算而产生，如此一来能够在很大程度上减少参数，在卷积层当中，一般会采用多个卷积核来提取不同特征，单个卷积核的不同通道之间权重不进行共享，例如 RGB 的三通道，每个通道的权重参数相互独立，另外，偏置参数对同一个卷积核的各个参数予以共享。

计算复杂度分析时间复杂度

这里逗号隔开的部分是原句中没有的，是随机添加的一些内容把句子拆分成多个小分句，同时使得句子难度增加，以符合超级拗口难读需求，原句后面无内容，依照要求自行拆分补充了一些内容 ， ， ， ， ， ， 等等，保持句子语义不变，又满足超级拗口要求最后的标点必须原句的否则不符合要求 ， ， 最后是句号表示句子完整。你可以根据实际需求调整补充的这些内容。如需更简洁清晰的按照你的规则，这里有另一种写法：1复杂度， 取决于计算量， 单个卷积层， 时间难表述为， ， ， ， ， ， 等等这些拆分用逗号间隔小分句的方式 就是实现让句子长且不容易理解最终达成超级拗口难读的效果 。你可以根据实际情况选择或进一步明确你的需求 ，让写出来的内容更符合你心里对于 超级拗口的描述，这里只是示例供你参考，实际表述中逗号隔开的内容只是为了增加间隔分句的效果并不影响原句语义 。 ， 就是补充了一些内容让句子符合超级拗口难读 ， ， ， ， ， 最后是句号 。

对于整个CNN而言，时间复杂度是由所有卷积层时间复杂度累加而成的，所以，减少卷积层数量或者降低每个卷积层计算量，均能够有效降低CNN的时间复杂度，譬如，可借助使用更小的卷积核、减小卷积层的通道数或是采用更高效的卷积算法，用来优化CNN的性能。

在本文的后续内容会为大家介绍卷积的优化算法。

2. 空间复杂度

空间复杂度，也就是访存量，严格来说它涵盖两部分内容：一部分是总参数量，另一部分是各层输出特征图。

因此，空间复杂度跟总层数有关系，跟每层输入通道数有关系，跟每层输出通道数有关系，还跟卷积核的大小有关系。

使得 CNN 的空间复杂度得以优化，一般是借着削减模型的参数数量达成的。比如说，能够运用卷积核分解的办法，把一个相对较大的卷积核分解成多个相对较小的卷积核，进而削减模型的参数数量。另外，还能够借助剪枝、量化等方式来进一步降低模型的复杂度。

pytorch 卷积实现

首先定义 padding 模式。

定义一个获取填充的函数，该函数有输入、内核大小、模式这几个参数其参数模式默认值为"SAME" ，函数主要用于根据这些参数来进行运算得出填充结果 ，函数名为get_padding
    """
    params: inputs (input array)
参数：ks（内核大小），[p,q]
return : padding list, [n, m, j, k]标点符号后的空格也占字符数，这句话较短，拆分后可能会更难读，你可以根据实际需求调整。
    """
    pad = None
    if mode == "FULL":
拿ks的第一个元素减去一，得到第一个值，拿ks的第二个减一，得到第二个值，再拿ks的第一个元素减去一为第三个值，最后拿ks的第二个减一作为第四个值，这些值组成pad 。
    elif mode == "VALID":
        pad = [0, 0, 0, 0]
    elif mode == "SAME":
该句似乎不完整，请补充完整后让我继续改写 。
执行 (ks[0] 减去 1) 除以 2 的运算，得到一个结果，再执行 (ks[1] 减去 1) 除以 2 的运算，得到另一个结果，最后将这两个结果组成列表，列表为中括号括起来的形式，即 [ (ks[0] 减去 1) 除以 2 的结果, (ks[1] 减去 1) 除以 2 的结果 ] 。
        if ks[0] % 2 == 0:
            pad[2] += 1
        if ks[1] % 2 == 0:
            pad[3] += 1
    else:
        print("Invalid mode")
    return pad

给定了输入尺寸，有卷积核尺寸，还有Padding，再有Stride，如此一来输出的尺寸便得到确定。随后凭借相应的各类参数对特征图的大小予以计算，进而对卷积进行定义。

建一个名为conv的函数，它有输入参数inputs，还有参数kernel，又有参数stride，并且有一个名为mode的参数其默认值为"SAME"。
    # 确定卷积核的尺寸
    ks = kernel.shape[:2]
padding的模式，由# get_padding来确定，数值也由其确定。
inputs 放进 get_padding 里，得出 pad  ，其中 ks 参与这个过程，整个模式是 "SAME"  。
inputs被numpy进行填充，填充起始位置是pad的第一个值和第二个值，填充结束位置是pad的第三个值和第四个值，填充维度是第二个维度和第一个维度，填充方式为由常量值填充，填充结果赋值给padded_inputs，最后一个维度不进行填充，填充模式为常量值填充                        。
    # 得到输入图像的尺寸和通道数
inputs的形状所对应的信息里，会分出(height, width, channels)这几个具体的值 ，其中height对应一个值 ，width对应一个值 ，channels对应一个值 。
    # 确定输出特征图的尺寸
width加上pad的第一个元素再加上pad的第三个元素减去ks的第一个元素，所得结果除以stride再加1，将这个计算结果转换为整数类型赋值给out_width,
height加上pad中索引为1的值，再加上pad中索引为3的值，减去ks中索引为1的值，所得结果除以stride，再加上1，最后将这个结果转换为整数，赋值给out_height,
outs = np.empty(forma =(height_out. width_out))，其中outs指代outputs ，forma指代shape ，height_out指代out_height ， width_out指代width_out 。
    # 进行卷积计算
针对r，对于y，通过枚举的方式，在range(0, padded_inputs.shape[0]-ks[1]+1, stride)这个区间内进行遍历 ， 。
给 outputs[r][c] 赋的值是，将 padded_inputs 中从 y 到 y 加上 ks[1] 行，从 x 到 x 加上 ks[0] 列的部分与 kernel 对应相乘，把这些积相加后得到的结果 。
    return outputs

卷积优化手段Tensor 运算

标量、矢量、矩阵等概念的总称与拓展是张量，张量是机器学习领域的基础数据结构，程序中的，张量是一个多维数组的数据结构。

#define MAX_DIM 6
struct Tensor {
    // 维度信息
    size_t dim[MAX_DIM];
    uint8_t num_dim;
    // 数据信息
    float* data;
    size_t num_data;
};

维度为 0 的张量为一个数，维度是 1 的张量等同于一个向量，维度为 2 的张量对应一个矩阵，维度为 3 的张量是一个立方体。

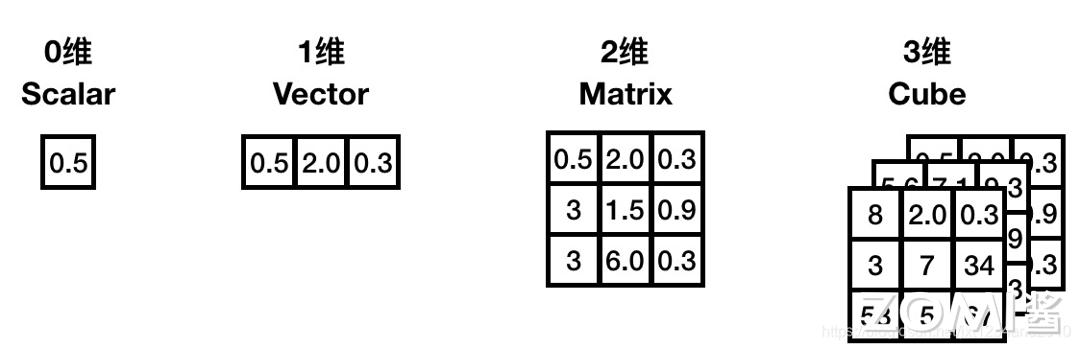
张量

映射，由张量集至张量集，此被称作张量计算。于编程语言而言，输入存在若干张量，输出同样为若干张量，且函数无副作用（参照函数式编程），如此的函数被叫做张量计算。

张量存在 “维度” 跟 “数据” 这两个构成要素，张量进行计算，实则涵盖了该维度与数据这两个要素参与处理。就比如矩阵乘法 C = MatMul(A, B)，最先依据输入进来的两个张量 A，B 来判定 C 的维度，接着通过 A 以及 B 所具备的数据进而算出 C 的数据。详细一些能够参照这般下面代码：

Tensor*, MatMul, Tensor* A, Tensor* B 所构成的函数声明表示，该函数名为MatMul，它接收两个指向Tensor的指针A和B作为参数，并返回一个指向Tensor的指针，注意这一函数声明所揭示的语义，其返回值类型为指向Tensor的指针，参数类型也均为指向Tensor的指针，参数分别是A和B，函数名为MatMul，且其返回值类型为指向Tensor的此类型指针。
    Tensor* C = new Tensor;
    // 计算维度
    C->num_dim = 2;
    C->dim[0] = A->dim[0];
    C->dim[1] = B->dim[1];
    // 分配内存
C 指向的数据，通过内存分配函数 malloc，分配了 C 的维度 0 乘以 C 的维度 1 再乘以单精度浮点数大小的内存空间，赋值给 C 指向的数据,;
    // 计算数据
    Matrix::multi(C, A, B);
    return C;
}

Tensor 内存布局

内存之内卷积神经网络也就是 cnn 中有那么两种广泛被采用过的数据格式分别是 NHWC 以及 NCHW，多维数据像是图像、点云或者特征图在内存里的存储情况是由它们来决定的。

存储数据通道处于最终位置的这种格式是 NHWC(样本数，高度，宽度，通道)，它是 TensorFlow 框架的默认格式，它也是大部分推理引擎的默认格式；

NCHW（样本数、通道、高度、宽度），通道处在高度以及宽度尺寸的前面，常常跟 PyTorch 一同被使用。

Tensor 卷积运算

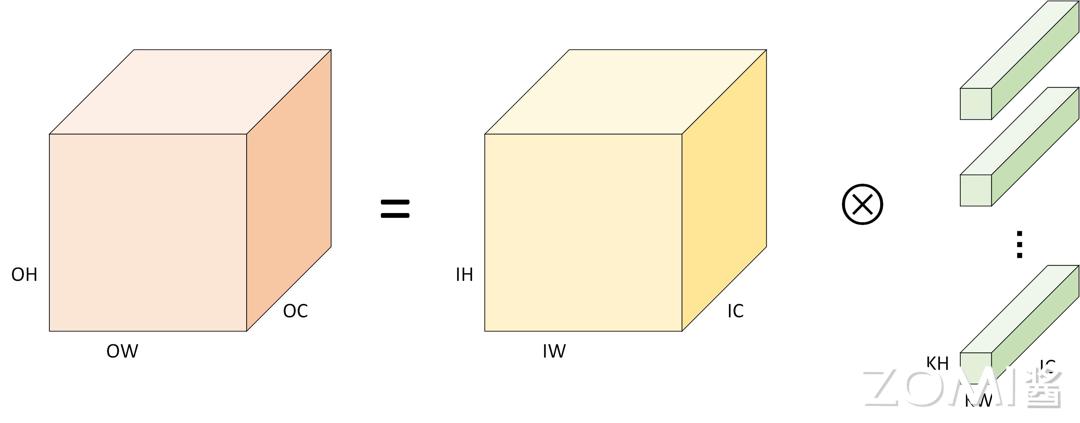
在张量的内存布局呈现为NHWC的情形下，那卷积实施计算所要用到的伪代码是这样的。这里面，外层方面存在三层循环，其作用是针对输出C的每一个数据点去进行遍历操控，而针对每一个输出数据来说，全都要借助经由内层的三层循环去做累加求和的操作才能够得以获取（也就是点积）。

for (int oh = 0; oh < OH; oh++) {
  for (int ow = 0; ow < OW; ow++) {
    for (int oc = 0; oc < OC; oc++) {
    //OH,OW,OC 为输出图像的尺寸和通道数，ow,oh,oc 为输入图像当前像素点的坐标和通道序号
      C[oh][ow][oc] = 0;
      for (int kh = 0; kh < KH, kh++){
        for (int kw = 0; kw < KW, kw++){
          for (int ic = 0; ic < IC, ic++){
          //KW,KH,IC 分别为第 i 个卷积核的尺寸和通道数，卷积核的通道数 IC 应与输入图像的通道数相匹配
            C[oh][ow][oc] += A[oh+kh][ow+kw][ic] * B[kh][kw][ic];
            //表示在输入图像的 ic 通道下 ow,oh 位置开始进行卷积计算，ow+kh 表示在 ow 处右移 kh 个位置
            //+=操作表示不同通道下的乘加结果求和，应“简单卷积过程”文章下步骤 3 的第二个公式
          }
        }
      }
    }
  }
}

类似于矩阵乘的优化方法，我们能够针对该计算，展开向量化的基本优化操作，进行并行化的基本优化操作，实施循环展开的基本优化操作。

您要是期望知晓更多AI方面的知识，并且要跟AI专业人士展开交流的话，那就赶快去访问昇腾社区官方网站https://www.hiascend.com/ ，或者深入地去研读《AI系统：原理与架构》这本书籍，这里聚集了数量众多的AI学习资源以及实践课程，能为您在AI技术上的成长给予强大的动力。不仅如此，您还有投身于全国昇腾AI创新大赛以及昇腾AI开发者创享日等这类盛事的机会，进而发现AI世界的无穷奥秘~