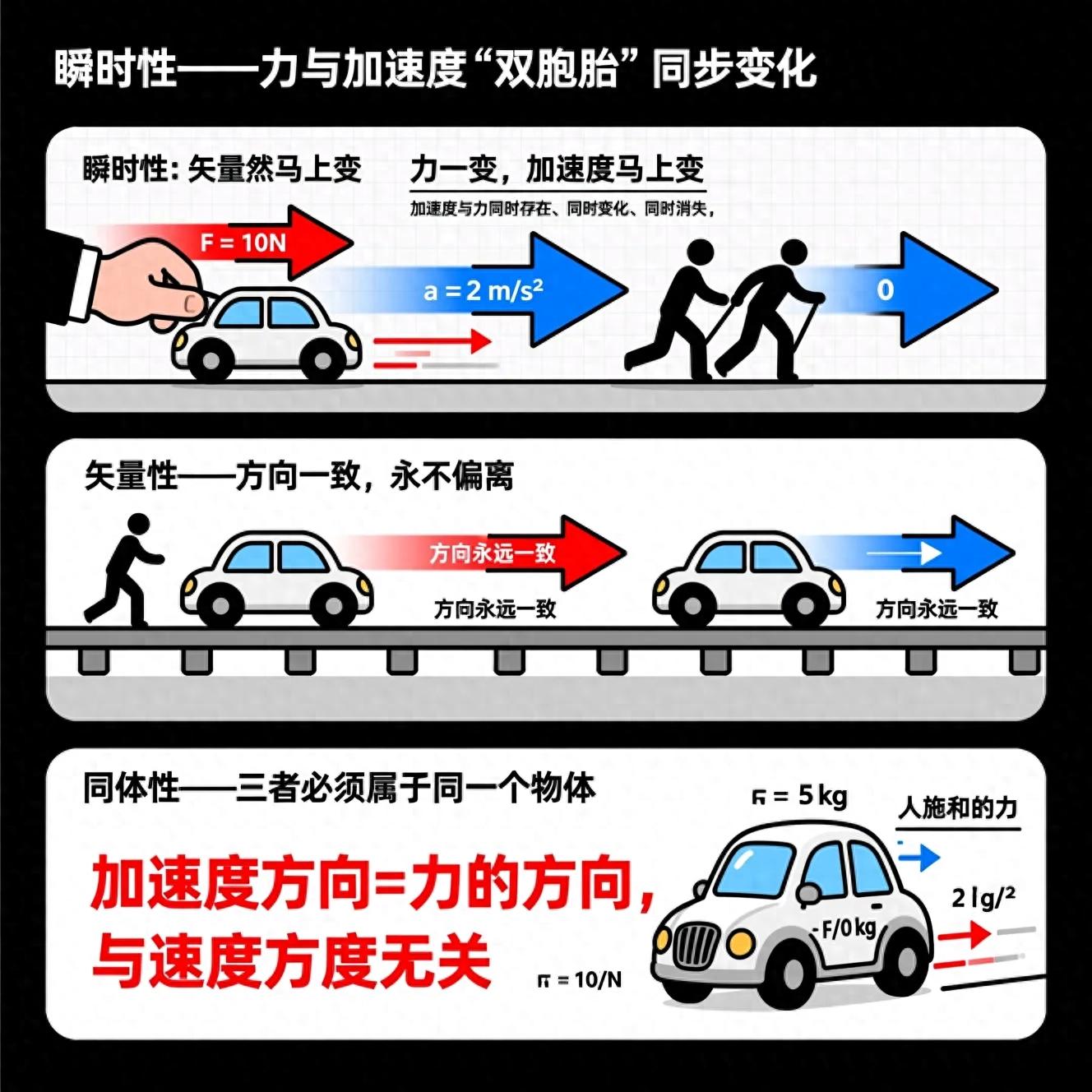
3.4函数的应用(一)课件-2025-2026学年高一上学期数学人教A版必修第一册
人教版2019年高中一年级数学教材必修第一册第三章,关于函数的内涵与特征第3.4节,函数的实际运用(初级篇)编号0203050604,精选范例(涵盖教材中的范例) 阐释要点 预备知识 引入情境 总结课堂 练习题目(包含教材中的习题)编号01掌握目标章节/目录学习目标1.可以运用函数原理构建数学模型来处理现实生活中的各种情形.这是本章节的重点内容2.需要挑选恰当的解题思路和对应的函数形式来应对现实中的各类问题.这是本章节的难点内容引入情境我们以前学习过的一次函数 二次函数 指数函数等都与现实生活存在密切关联通过具体案例可以认识它们的各种用途,了解借助函数形式处理现实问题的方法与技巧。很多人觉得数学很乏味,对今后生活帮助不大。其实数学与我们的生活息息相关,数学最初也是为了满足生活需求而逐步完善的。比如用手机付款,比如看到摩天大楼,比如关注神舟系列航天器发射成功,这些都与数学和数学模式紧密相关。(1)线性函数形式:,,(2)倒数型函数形式:,,(3)抛物线型函数形式:,,,(4)指数型函数形式:,,,,(5)混合型函数形式:这种形式其实是前几种形式组合而成,因此使用场景非常普遍。常见的数学形式有哪些?以下通过具体案例来感受它们的多样应用,学习运用函数形式处理现实问题的思路与方法。知识探索课本范例例1 假设小李全年总收入为x元,应缴个税金额为y元,已知个人社保和公积金占收入比例分别是8%、2%、1%、9%,专项附加扣除为52800元,其他依法扣除项为4560元。(1)推导y与x的数学关系;(2)如果全年总收入为249600元kaiyun.ccm,计算全年个税总额是多少?解:根据个人应纳税所得额的公式,当t等于零时,x等于146700,依照规定,若x在零到146700之间,t为零,因此,个人应纳税所得额t关于综合所得收入额x的函数表达式为,当x在零到146700范围内,t等于零,相应地y也等于零;当x超过146700时,t大于960000,所以y等于t乘以百分之四十五减去181920,即y等于0.36乘以x减去234732,因此,函数表达式为,当x等于249600时,y等于0.08乘以249600减去14256,计算得y等于5712,所以小王全年需要缴纳的综合所得个税税额为5712元,结论是,依据个人收入状况,借助上面得到的个税和月工资关联的函数表达式,可以直接计算出应缴纳的个税,759080例2.一辆汽车在某段路线中的平均速度v(单位为千米每小时)与时间t(单位为小时)之间的关系如图(1)所示,(1)计算图(1)中阴影部分的面积,并阐释所求面积的实际意义,9080706050403020105065(2)假设这辆汽车的里程表在汽车行驶这段路线前的读数为2004千米,尝试建立行驶这段路线时汽车里程表读数s(单位:千米)与时间t的函数表达式,并绘制相应的图像,能否根据图像描绘出汽车行驶路程关于时间变化的图像,图(1)分析:当时间t在内变动时,对于任一时刻t都有唯一确定的行驶路程与之对应。根据图(1),在时间段
0,1),
1,2),
2,3),
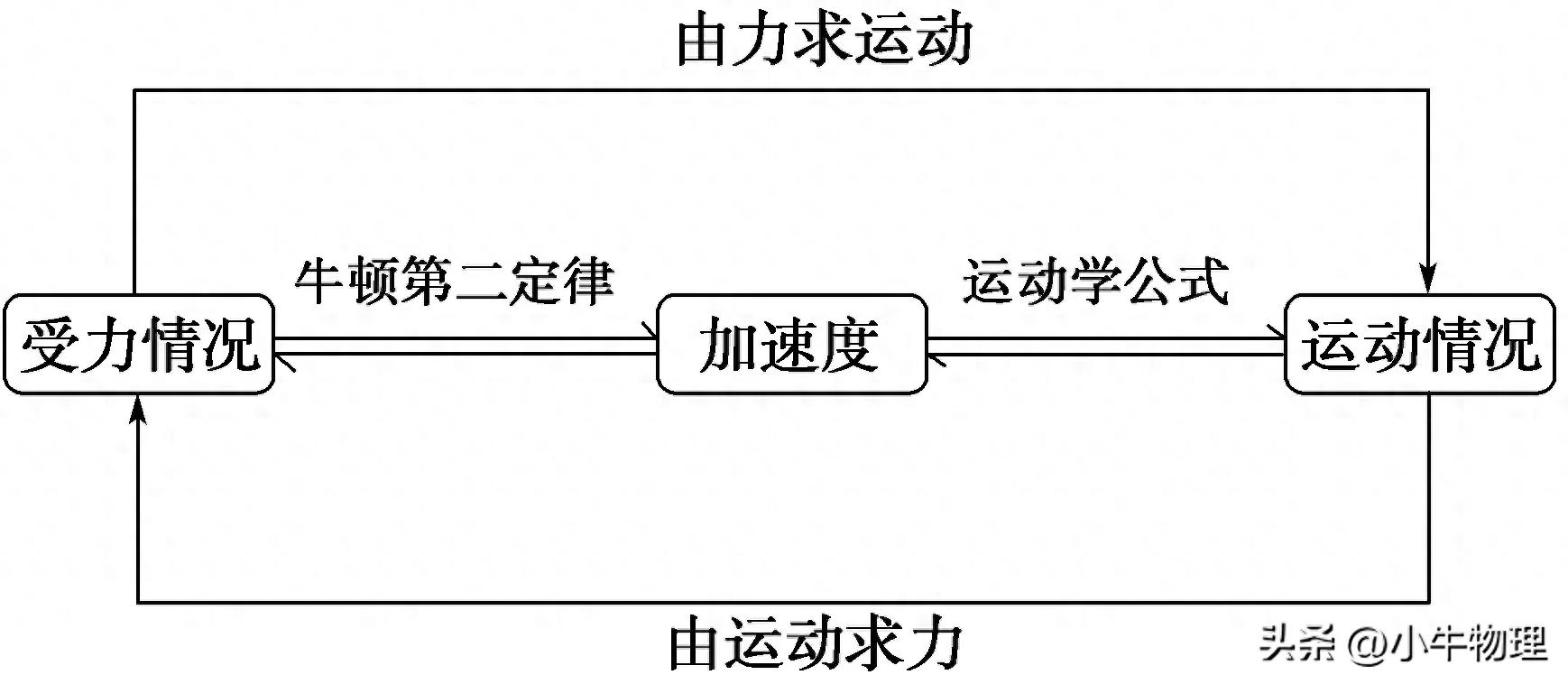
在3,4段中,车辆的平均速度分别是50千米每小时,80千米每小时,90千米每小时,70千米每小时,60千米每小时,因此每个时段内,前行的距离和经过的时间的关联也不相同,必须分段说明。解:第一段,从0到1小时,行驶了50千米,第二段,从1到2小时,行驶了80千米,第三段,从2到3小时,行驶了90千米,第四段,从3到4小时,行驶了70千米,第五段,从4到5小时,行驶了60千米,总共行驶了360千米。根据图示,可以知道在0到1小时,行驶距离是50乘以时间,在1到2小时,行驶距离是200加上50乘以时间减去1,在2到3小时,行驶距离是205加上80乘以时间减去2,在3到4小时,行驶距离是213加上90乘以时间减去3,在4到5小时kaiyun全站网页版登录,行驶距离是222加上70乘以时间减去4,最后是229加上60乘以时间减去5,这个函数的图像如图2所示。图2课本练习1,如果用模型来描述汽车在紧急刹车后滑行的距离y米和刹车时的速度v千米每小时之间的关系,某种型号的汽车在速度为60千米每小时时,紧急刹车后滑行的距离是20米,在限速为100千米每小时的高速公路上,这辆车紧急刹车后滑行的距离是50米,需要判断这辆车是否超速。【解】根据题目要求,将数值对代入公式中,可以计算出,由此得出公式形式,在特定条件下,可以求得,由于,因此这辆车并未超速行驶。2.某宣传机构需要为客户制作一块周长为六十米的矩形宣传板,怎样规划这块宣传板的尺寸才能使其面积达到最大值?【解】假设广告牌的长度是t米,那么它的宽度就是30减去t米,面积S经过公式化简后,得出最优解,即当长度为15米,宽度也等于15米时,能够获得最大面积,这个最大值是225平方米。3.某企业制造特定商品的固定开销(包括租赁场地和设备费用以及水电支出等)为150万元,每件商品的生产费用是2500元,销售价格是3500元。如果该企业生产的产品全部能够成功售出。(1)设定总开销为W万元,平均到每件商品上的单位成本是y万元,销售总额为S万元,总利润是P万元,分别推导出它们与产品数量t的数学表达式。【解】依据题目信息可知 (2)依据计算得出的函数图像,对该企业的经济收益进行简要探讨。题型分类解析题型1 一次函数、二次函数的实际应用1.某区域电力公司为激励小型企业提升夜间用电量,制定了在月度夜间计费时段内通过按用电量分级计收电费的政策,夜间月度用电量与对应电费金额(单位:元)的函数关系如图所示,当夜间月度用电量达到特定数值时,应支付的电费为多少?A.130元 B.140元 C.150元 D.160元解析 结合函数图像可以判断,当夜间月度用电量处于该数值时,用电量与电费之间呈现线性关系,设函数为,系数分别为,当;当,则解得此时,。所以当,。因此选择D。2.[江西上饶2025高一月考]你是否了解古人对烟花的看法?那是朱淑真《元夜》中的“火树银花映眼红”,也是隋炀帝笔下的“灯树千光映照,花焰七枝绽放”。烟花,虽是无根之花,是短暂之花,却在升至顶点时绽放,用其辉煌的瞬间换取人们热烈的掌声。已知某种烟花距离地面的高度(单位:米)与时间(单位:秒)的关联式为 ,那么烟花在撞击后爆开的时刻是()AA.第4秒 B.第5秒 C.第3.5秒 D.第3秒解析 根据题意, ,则当 时,烟花达到顶点,即爆开的时刻是第4秒。故选A。163.[陕西西安2025高一期中]某小型服装厂生产一种风衣,日销售量件(单位:件) 与售价(单位:元/件)的关联为,生产件所需成本 (单位:元),当工厂日收益不小于1 000元时,该厂日产量最少生产风衣的件数是____。10解析 根据题意,设该厂日收益为元,则开元棋官方正版下载,当工厂日收益不小于1 000元时,即 ,即 ,解得且 。故该厂日产量最少生产风衣的件数是10。174.[吉林长春多校2025高一期末联考]统计显示,一名工人组装第 件产品所用的时间(单位:分)为,为常数。已知工人组装第4件产品用时30分钟,组装第 件产品用时5分钟,那么和 的值分别是()CA.75,25 B.75,16 C.60,144 D.60,16题型2 分段函数的应用解析 根据题意可得 ,故则 故选C。185.[广东茂名七校2024高一联考]某建材商场国庆期间开展促销活动,规定:如果顾客选购物品的总金额不超过1 000元,那么不享受任何折扣优惠;如果顾客选购物品的总金额超过1 000元,那么超过1 000元部分享受一定的折扣优惠,折扣优惠按如下表格累计计算。 可以享受折扣优惠金额 折扣优惠率 不超过500元部分 超过500元的部分 若某人在此商场购物得到的折扣优惠金额为40元,则他实际所付金额为________元。1 610解析 设顾客选购物品的总金额为元,得到的折扣优惠金额为元,则当时, 。当时, ,令,得,解得 ,不符合题意。当时, ,令,得,解得 ,符合题意,所以他实际所付金额为 (元)。196.某公司租地建仓库,已知仓库每月占用费 与仓库到车站的距离成反比,而每月车载货物的运费与仓库到车站的距离成正比。据测算,如果在距离车站处建仓库,这两项费用, 分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站()AA.处 B.处 C.处 D. 处题型3 幂函数和对勾函数的应用解析 设仓库到车站的距离为,由题意可设,,其中 。由当时,两项费用,分别是2万元和8万元,可得, 。故,当且仅当,即 时取等号,故选A。207.(多选)[河北保定部分学校2025高一联考]在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量单位:与管道的半径单位: 的四次方成正比,当气体在半径为的管道中时,流量为 ,则()ACA.当气体在半径为的管道中时,流量为 B.当气体在半径为的管道中时,流量为 C.要使得气体流量不小于,管道的半径的最小值为 D.要使得气体流量不小于,管道的半径的最小值为 解析 依题意可设, 为常数。当气体在半径为的管道中时,流量为,所以,解得 ,则.当时, ,故A正确,B错误。由,解得,故C正确,D错误。故选 。218.[山东部分学校2024高一联考]某文旅企业准备开发一个新的旅游景区,前期投入200万元,若该景区开业后的第一年接待游客万人,则需另投入成本 万元,且 该景区门票价格为64元/人。(1)求该景区开业后的第一年的利润(万元)关于人数 (万人)的函数关系式.(利润 收入-成本)【解】该景区的门票收入为 万元,则利润最大利润为多少?当时,二次函数图象朝下伸展,对称轴为一条直线,所以;当且仅当,也就是,等号才会成立,因此;总而言之,当该景区在开业后的第一年接待游客数量达到20万时,能够得到的利润最大,最高利润为260万元.239.(多选)[浙江台金七校2025高一期中联考]如图①描绘了某条公交线路收支差额(即营运所得票价收入与付出成本的差)和乘客数量之间的关系图.由于目前该条公交线路处于亏损状态,公司相关人员提出了两种调整方案,如图②③所示.图①图②图③那么下列说法中准确的有()BCA.图②的方案:增加成本,同时提升票价 B.图②的方案:减少成本,而票价维持不变C.图③的方案:提高票价,而成本维持不变 D.图③的方案:提升票价,同时降低成本解析 依据题意和图②可知,两条直线平行意味着票价保持不变,直线向上平移表示当乘客数量为0时,收入为0,但支出减少了,表明此方案是降低成本并维持票价不变,所以A不正确,B正确;从图③可以看出,当乘客数量为0时,支出保持不变,但直线的倾斜度变大,即在相同乘客数量下收入增加,即票价提高了,说明此方案是提高票价并维持成本不变,因此C正确,D不正确.所以选择 .易错警示 对于函数图象的认识必须精确,特别是对每个变化点的含义及其数值意义要理解透彻.易错点 对函数图象的认识不充分而导致的错误24课堂小结1.解有关函数的应用题,应当首先考虑选择哪种函数作为模型,然后建立其表达式.求表达式时,通常采用待定系数法,需要充分发掘题目的隐含条件,并充分利用函数图形的直观特性.2.数学建模的过程图示如下:$$