【初中数学】勾股定理必考,相关知识点+4种简单应用!
免费进学习资料群!

以微课堂学习群
奥数国家级教练与四名特级
教师联手执教
写在前面:
夏季休假时段可不单单是被用以放松嬉戏的,更是被用以实现“弯道超越”的。在暑假做到比别人先行一步,开学之时就能在一众同学中领先一段路!若开学之际不想在他人之后,那在暑假就要赶快着手预习。现下要和大伙分享的是预习内容,初中数学方面的【勾股定理】属于必考范畴,与之相关的知识点以及4种较为简易的应用方法 !
基础知识点
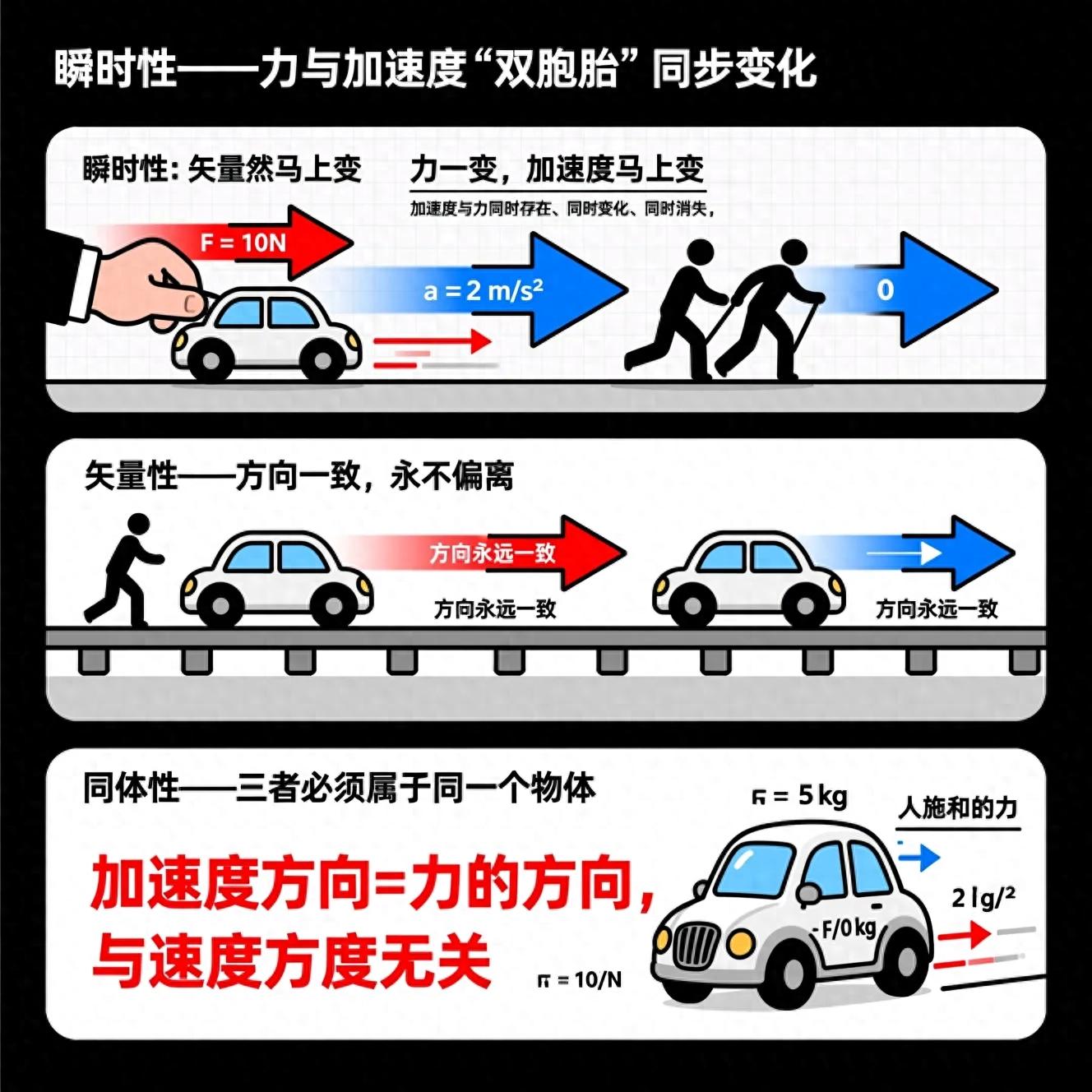
勾股定理,直角三角形当中,存在这样一种关系,两直角边分别为a、b ,其平方和,等于斜边c的平方,也就是a2+b2=c2 。
要点诠释: 勾股定理, 反映了直角三角形三边间关系, 是直角三角形较重要之性质的其中一个, 其主要应用:
(1)已知直角三角形的两边求第三边
(2) 已知,存在一种情况,涉及直角三角形,其中一边与另外两边有着某种关系,在此种情况下,要去求出直角三角形的另外两边 。
(3)利用勾股定理可以证明线段平方关系的问题
1、勾股定理在网格中的应用
已知,正方形边长是1,(1)如此图a,能算出正方形对角线之长为根号2.
①分别求出图(b),(c),(d)中对角线的长
②九个小正方形排成一排,对角线的长度
(用含n的式子表示)为( )
分析:借助于网格,构造直角三角形,直接利用勾股定理.
2、勾般定理在最短距离中的应用
例2 如图所示,已知C这个点是SB的中点,圆锥的母线长度为10cm,其侧面展开图呈现为一个半圆,A所处在的位置有一只蜗牛想要吃到C处的食物,它能够选择的路径只能是沿着圆锥曲面爬行,请你计算出蜗牛爬行的最短路程。
求解几何图形两点间最短距离问题时,要把几何体表面进行展开,还要去求展开图中两点间的距离,展开过程里必须弄明白所要求的是哪两点间的距离,以及它们在展开图里的相应位置.句号不能删除。

在对于求立体几何图形相关问题进行点评时,通常是借助平面展开图,把它化作平面图形问题,进而展开求解.
3、勾股定理在生活中的应用
例如3,如图所示,学校存在一块呈现长方形的花园,存在较少数部分同学为做到避开拐角从而去走“捷径”,于校园范围之内走出了一条“路”,要请同学们进行计算,实际上这些同学仅仅是少走了多少步路这件事情,然而却踩伤了花草,(假设1步为0.5m)。

评论指出,以走“捷径”问题作为起始点是常常会碰到的状况kaiyun官方网站登录入口,在对勾股定理予以考察的同时,还融入了环保方面的教育,即少迈几步路途,便能够留存下一片令人期待的绿色。
有这样一个事例,事例是小华想明白自家门前小河的宽度,所以就依照以下方法测得了如下这些数据,数据是小华在河岸边挑选出点A,在点A的对岸选定一个参照点C,观测得到∠CAD等于30°,小华沿着河岸向前行走30m挑选点Bkaiyun全站app登录入口,并且观测得到∠CBD等于60°。请依据以上数据,利用你所学的数学知识kaiyun.ccm,帮小华计算小河的宽度。

点评:这道题目考查的是直角三角形的应用,解答此问题的关键之处在于,画出示意的图形,把问题转变成解直角三角形的问题。
免费进学习资料群!

以微课堂学习群
奥数国家级教练与四名特级
教师联手执教。