0斐波那契数列的诞生与兔子问题
斐波那契数列,堪称数学领域的一颗明珠,凭借其非凡的特性与诸多用途,吸引了众多数学迷的关注。在自然现象的奇妙法则中,在生活细节的微妙之处,它都能找到踪迹,对世界产生着影响。
是自然景象与数字规律的奇妙融合,抑或是数字法则阐明了自然风貌的精妙之处?让我们共同发掘斐波那契的独特价值所在。这位意大利学者出身显赫门庭,他的学术生涯极富传奇性,不仅足迹遍布东方阿拉伯诸多都会,更潜心钻研印度—阿拉伯的十进制体系,特别是对数字零的巧妙运用。这些全面而细致的钻研,让他在数学、代数、几何等多个学科都获得了非凡的建树,最终成为中世纪数学界的杰出人物。
不过kaiyun全站登录网页入口,在那个时代,意大利社会大多还在运用罗马数字进行运算,唯有斐波那契敏锐地察觉到印度—阿拉伯数字体系的精妙之处和便捷特点。他不仅大力倡导这种新方法,还亲身实践,从而为数学学科的发展促成了划时代的进步。
0斐波那契数列的诞生与兔子问题
《算盘书》里,斐波那契不仅说明了印度—阿拉伯数字,也演示了它们的计算方式,还提出了一个有趣的数学议题——兔子繁衍难题。这个议题不仅引起了大众对数学的关注,更促进了数学学界的进步。为了表彰斐波那契的成就,人们把这个序列称作斐波那契数列。
这个数列的来历与1202年意大利数学家列奥纳多·斐波那契研究的兔子繁衍现象有关。他当时构建了一种序列,其目的是计算兔子数量随时间的变化。该序列以特殊形式揭示了自然界中生命成长的模式,因此成为数学研究中的一个关键成果。
要透彻认识斐波那契数列,可以把它和兔子繁衍现象联系在一起考虑。假设开始时有一对新生的小兔子,等它们长大具备生育能力后,每个月就会生育一对小兔子。依照这个模式,在50个月之后,总共会有多少对兔子呢?这个问题的答案,就包含在斐波那契数列的规律里。
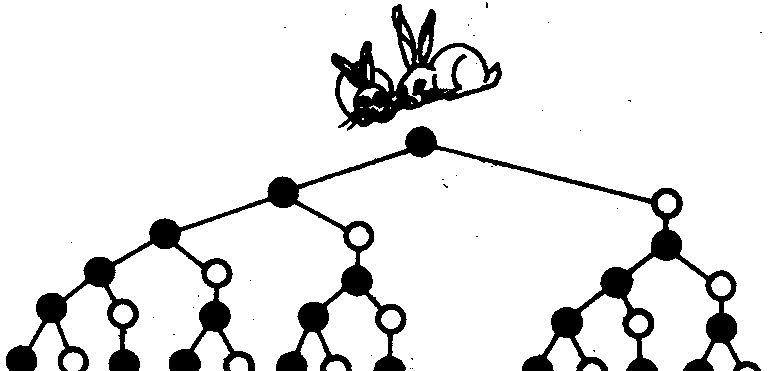
时间(月)
初生兔子(对)
成熟兔子(对)
兔子总数(对)
55
# 2斐波那契数列:自然界的神奇韵律
伽利略有句名言,称自然界的书是用数学的语言写成的。在辽阔的宇宙中游走,很容易察觉到斐波那契数列的痕迹遍布各处。比如冬日仙人掌小球上的小刺,以及食肉植物芦荟上的“斐波那契黄金角”螺旋,还有城市街道旁枝丫树叶的奇特分布,都暗藏着斐波那契数列的数学魅力。向日葵的花盘构造和瓜子排列方式,同样遵循着这一古老数学原理,呈现出由核心向边缘逐步延展的均衡美感,这种奇妙景象,无不揭示了斐波那契数列在自然界中的非凡影响力。

向日葵的花瓣有两种方向旋转着分布,朝一个方向旋转的花瓣数量和朝另一个方向旋转的花瓣数量,总是符合相邻两个数字的规律,这种数字规律属于斐波那契数列。
松树的松果有着与众不同的旋涡式分布,其鳞片数目依照斐波那契数列的顺序排列。类似地,不少花朵的花瓣数量也暗含这一数列的规律,比如兰花拥有三片花瓣,桃花有五片,飞燕草达到八片,万寿菊有十三片,紫苑则拥有二十一片,这些现象都充分展现了斐波那契数列所蕴含的数学魅力。我们感到十分惊讶,自然界的诸多神奇景象,竟然和斐波那契数列有着惊人的吻合。
0设计的“灵感之源”
经过细致研究,我们察觉到斐波那契数列和黄金分割比之间存在十分显著的对应关系。这个数列,它由若干个特定数值排列而成,其相邻两项的比值居然和黄金分割比非常接近。这一现象,无疑为创作者们开拓了丰富的构思途径。
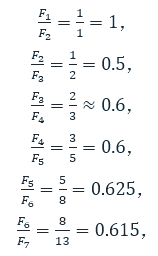
两个相邻数值的比率,要么超出那个特定的比例,要么低于那个特定的比例,形成一种富有变化的和谐美感。
而且这个比例持续向黄金分割点靠拢,呈现出一种几乎无瑕的动态和谐之美。

品牌设计的灵感之源
苹果公司的标志并非仅是一个被咬掉一部分的苹果形象那么简单,仔细研究可以发现,其中的曲线和几何线条都展现了数学的精确和条理。所谓的“黄金螺旋”构思,其基础来源于斐波那契数列。巴西Boticario企业商标也精妙地运用了“黄金螺旋”的构造方式。在《达·芬奇密码》这部著作里,所谓“黄金螺旋”同样扮演了核心提示的角色,由此可知它对于设计及美学领域具有相当的价值。
斐波那契序列不仅是数学概念,也是一种美学思想。将它运用到品牌形象塑造中,可以激发大众的审美共鸣,散发出温和友善的氛围。此类构思不仅充分展示了品牌的艺术内涵,而且与机构的中心宗旨高度一致。

以斐波那契序列作为构思基础注入品牌内涵,再将其运用到具体商品之中,能够精准对接大众多样的审美偏好,使人感受到一种温和而友善的氛围。此类构思不仅让品牌的艺术水准得以充分彰显,还与企业的根本立场和目标形成了高度统一和协调。
0斐波那契数列:一门实用的艺术
斐波那契数列在工业制造中促成了时栅测量技术的出现。该数列在管理学和运筹学方面用途广泛,例如可用于构建流量分析模型。现代信息电子技术领域借助该数列的规律,研发出一种创新的半导体结构化循环低密度奇偶校验数编码方案。此方案既简化了集成电路的设计流程,又确保了卓越的纠错管理能力。
金融行业里,斐波那契数列也显现了其特殊作用。借助这个数列,能够依据关键转折点预测后续市场动向。股票交易中,这种技巧称作斐波那契循环。利用详尽的时间图表,可以准确估算出未来波段运行里,市场整体涨跌的幅度以及过程时长。值得注意的是,斐波那契数列优化技术已构成当代金融学科的核心要素。
0探寻数学文化的“灯塔”
数学课本里的“阅读与思考”部分,好比一束照亮数学领域的光亮。借助这些内容,能够让我们透彻认识数学学科同人类社会进步的紧密联系,可以探寻数学演进的来龙去脉,能够体会数学传统的博大精深。这些材料不仅开阔了我们的数学眼界,还点燃了我们对数学领域探求真知的浓厚兴趣。
十八四三年,Binet这位数学家构思出一种方程式,这种方程式以精妙方式揭示了数学领域里非整数与整数的内在关联性。虽然这种知识不在高考考察之列,但斐波那契数列的检测关键在于其连续推演的基本理念。为了更透彻地把握这个理念,可以借鉴下列模拟考题来学习
意大利数学家列昂纳多·斐波那契是欧洲最早对印度—阿拉伯数学理论进行系统研究的学者之一。斐波那契数列,被称作数学领域中最具美感的序列,其构造方式为:序列的前两项分别取值为1,从第三项起,每一项的数值等于它前面两项数值的总和,即公式an等于an-1加上an-2,其中n大于等于3,且n属于自然数集。假设把数列的各个元素看作一个个小方块,每个小方块的一边长度是1,那么前n个元素所占据的空间大小Sn,还有每条螺旋线与其周围的正方形形成的扇形区域面积Cn,都变成了分析的重点。现在,我们要来研究一下和这两个面积有关的几条性质。
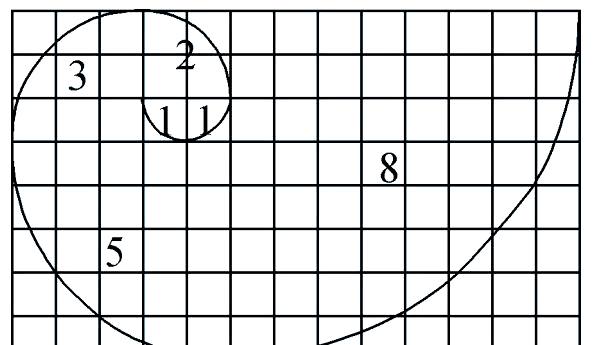
这道题目以斐波那契数列作为考察基础,意图检测考生的文本解析水平以及数列求和的掌握程度,但相当一部分学生面对它时心存顾虑。依据斐波那契数列的内涵,能够推演出涉及an的递进关系式:当n大于等于3且属于自然数时,an等于an-1与an-2之和,即an=an-1+an-2;当n大于等于2且属于自然数时,an+1等于an与an-1之和,表现为an+1=an+an-1;同时,对于所有自然数n,an+2的值等于an+1与an的总和,可以写成an+2=an+1+an。这些公式为我们提供了深入探讨斐波那契数列的基础。
根据斐波那契数列的相邻两项关系式,当n大于等于2时,a_{n+1}的值等于a_{n}与a_{n-1}的和,由此可以得出a_{n}等于a_{n+1}减去a_{n-1},同样适用于n大于等于2的情况。根据这个公式,我们可以把数列S_{n}等价转换成S_{n},它等于a_{1},再加上a_{3}与a_{1}的差值,接着是a_{4}和a_{2}的差值,后面依次类推,直到加上a_{n+1}和a_{n-1}的差值。经过再次简化,我们得到S_{n}等于前n项中第1, 3, 4, …, n+1项之和减去前n项中第1, 2, 3, …, n-1项之和,等于第n项与第n+1项之和减去第2项,最终等于第n+2项减去1。
奇数项和偶数项的累计值可以分开计算,奇数项的累计值是a_{1}+a_{3}+a_{5}+⋯+a_{2n-1},这个式子可以改写成a_{1}+(a_{4}-a_{2})+(a_{6}-a_{4})+⋯+(a_{2n}-a_{2n-2}),最后等于a_{2n}。同样地,偶数项的总和是a_{2}加上a_{4},再加上a_{6},一直到a_{2n},这个总和等于a_{2n+1}减去1。
此外,我们能够借助斐波那契数列的连续关系式开yun体育app官网网页登录入口,计算出各项的平方总和。比如,针对任意的项数n,可以得到a_{n}^{2}等于a_{n}乘以a_{n+1}减去a_{n-1},这个值其实等于a_{n}a_{n+1}再减去a_{n}^{2}与1的和。运用同样的方法,能够导出诸多等式,例如a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+往后直到a_{n}^{2}等于a_{n+1}乘以a_{n},这些等式有助于我们深入研究斐波那契数列各项平方的总和。
根据归纳出的公式和多次演算,可以总结出有关斐波那契数列累加值和各项平方总和的若干定理。这些定理有助于揭示斐波那契数列的内在规律,同时也为处理相关数学问题创造了有效方法。
0数学遗产的“启迪”
斐波那契数列在数学界影响深远,物理、化学、生物等多个领域也深受其用,它被用于解决准晶体构造、股市研究、力学体系稳固性等实际问题。不仅如此,美国还创办了《斐波那契季刊》这份数学期刊,专门发表关于该数列的研究成果,由此可知其学术地位很高。但是,这个古老的数列还存在一些未解之谜,比如有无穷多个斐波那契数是素数,斐波那契数列中完美数和完全平方数的数量是多少,这些问题仍需数学家继续研究。
斐波那契数列并不只存在于学术领域kaiyun.ccm,它与自然息息相关,广泛渗透到我们日常的实践和生存活动中。



