斐波那契的生活应用有哪些？

斐波那契的生活应用：

斐波那契数列里的数字，在现实世界中很常见，比如松果的鳞片分布，凤梨表皮的纹路，树叶的叶序，某些植物的花瓣数量，像向日葵的花瓣就是典型例子，还有蜂巢的结构，蜻蜓的翅膀形状，甚至与超越数e有关联，可以引申出更多内容，此外还有黄金矩形，黄金分割比例开元棋官方正版下载，等角螺线，以及十二平均律等领域。

斐波那契数列的规律也能在植物的生长部位观察到。比如，考察树木的枝干，选定一片叶子作为基准点标记为0号，接着按顺序计算叶子数量（假设叶子没有破损），数到与基准点正对着的另一片叶子，这个过程中经过的叶子数量通常就是斐波那契数。叶子从一个位置移动到与之相对的下一个位置，这个过程被称为一个周期。

矩形面积的价值体现在很多方面，比如：

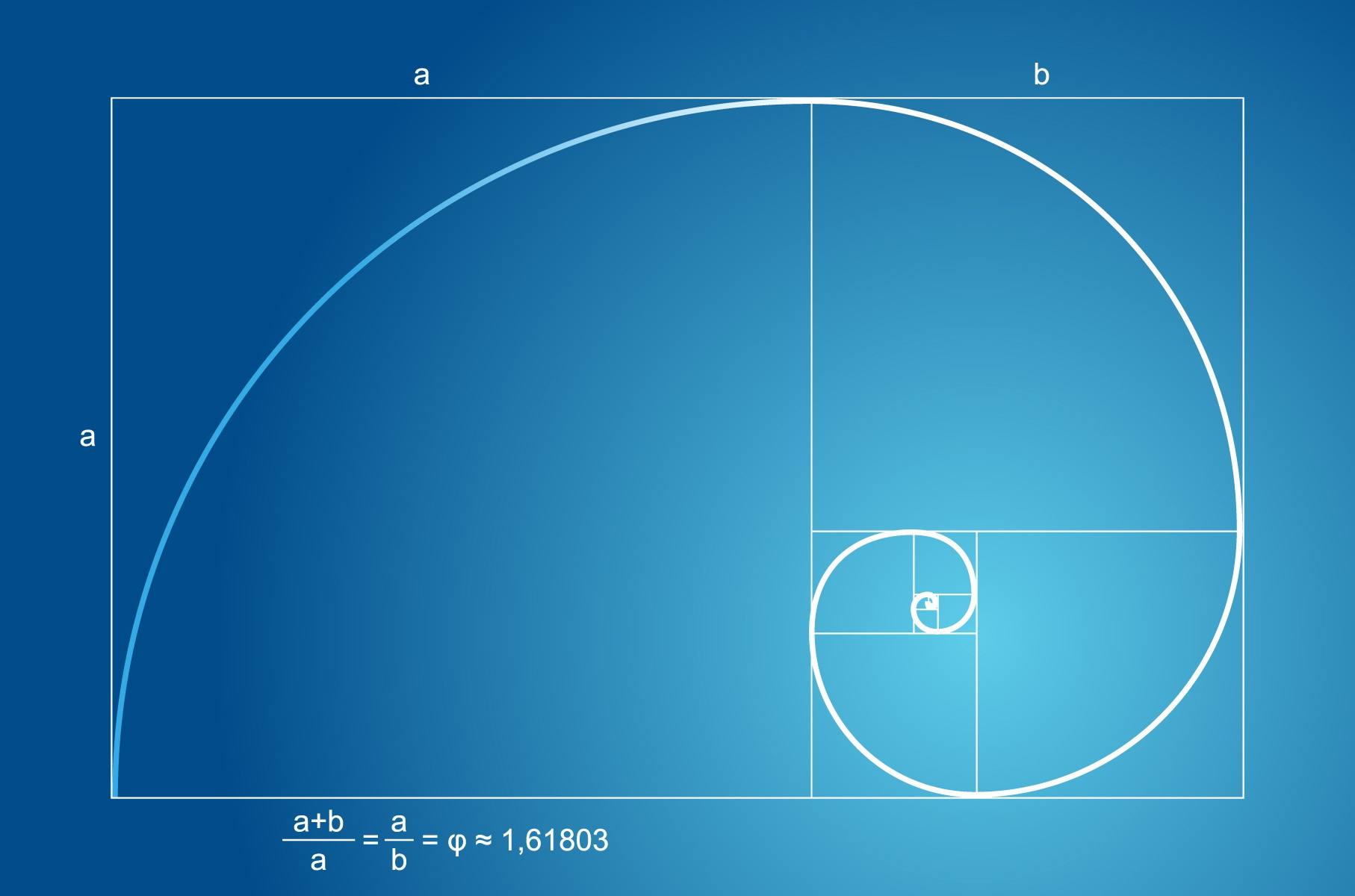
斐波那契数列跟矩形面积的形成有关，因此可以引申出该数列的一个特性。该数列初始几项的平方，可以看作是不同边长的正方形。依据斐波那契的递推关系，这些正方形能够组合成一个大的矩形。所有小正方形的面积总和，正好等于大矩形的面积。

在科学领域没有被广泛应用。

扩展资料：

斐波那契数列的特性：

从第二项起开yun体育app官网网页登录入口kaiyun全站网页版登录，每个偶数项的平方值，比它相邻的前后两项相乘的结果小1，而每个奇数项的平方值，则比它相邻的前后两项相乘的结果大1。

第二项的平方数比它左边那个数和右边那个数的乘积小1，第三项的平方数比它左边那个数和右边那个数的乘积大1。

斐波那契数列在自然科学的其他分：

比如，树木长高，因为新生的枝条，通常要一个“休养”阶段，助其自身发育，然后才能生出嫩芽。因此，一棵小树在一段时间间隔，比如一年，后生出一条新枝；第二年那新枝“休养”，老枝继续发芽；接着，老枝和“休养”过的枝条同时发芽，而当年生的枝条则次年“休养”。

因此，一棵树不同年份的枝条数量，就组成了斐波那契数列，这一现象，在生物学领域被称为“鲁德维格定律”。

参考资料：