牛顿第二定律

牛顿第二运动定律，即牛顿的运动定律之二，通常表述为：物体的加速度程度与施加的力成正比，与物体的重量成反比，并且与物体重量的倒数呈现正相关关系；同时，加速度的指向与力的方向保持一致。艾萨克·牛顿在1687年所著的《自然哲学的数学原理》中提出了这一重要定律。牛顿的第二运动定律与第一、第三定律相辅相成，三者共同构成了牛顿运动定律体系，全面揭示了经典力学领域内运动的基本法则。

定律定义

牛顿在《自然哲学的数学原理》发表的原始表述：

质点在受到外力影响时，其动量随时间的推移呈现出变化的趋势，这种变化率与质点所承受的外力之间存在直接关系，且两者方向一致；这一关系可以用特定的公式来表示。

常见表述：

物体的加速度程度与所受的合外力直接相关，且与物体的质量呈反比关系，即与质量的倒数成正比。加速度的指向始终与合外力的方向保持一致。牛顿的第二运动定律能够通过比例关系式进行表达，形式为F=ma或F=km*a；亦可用等式形式表示，即合外力等于比例系数k乘以质量m再乘以加速度a，即∑F=kma；此等式仅在合外力以牛顿为单位、质量以千克为单位、加速度以米每平方秒为单位时成立。

定律特点

牛顿第二运动定律有五个特点：

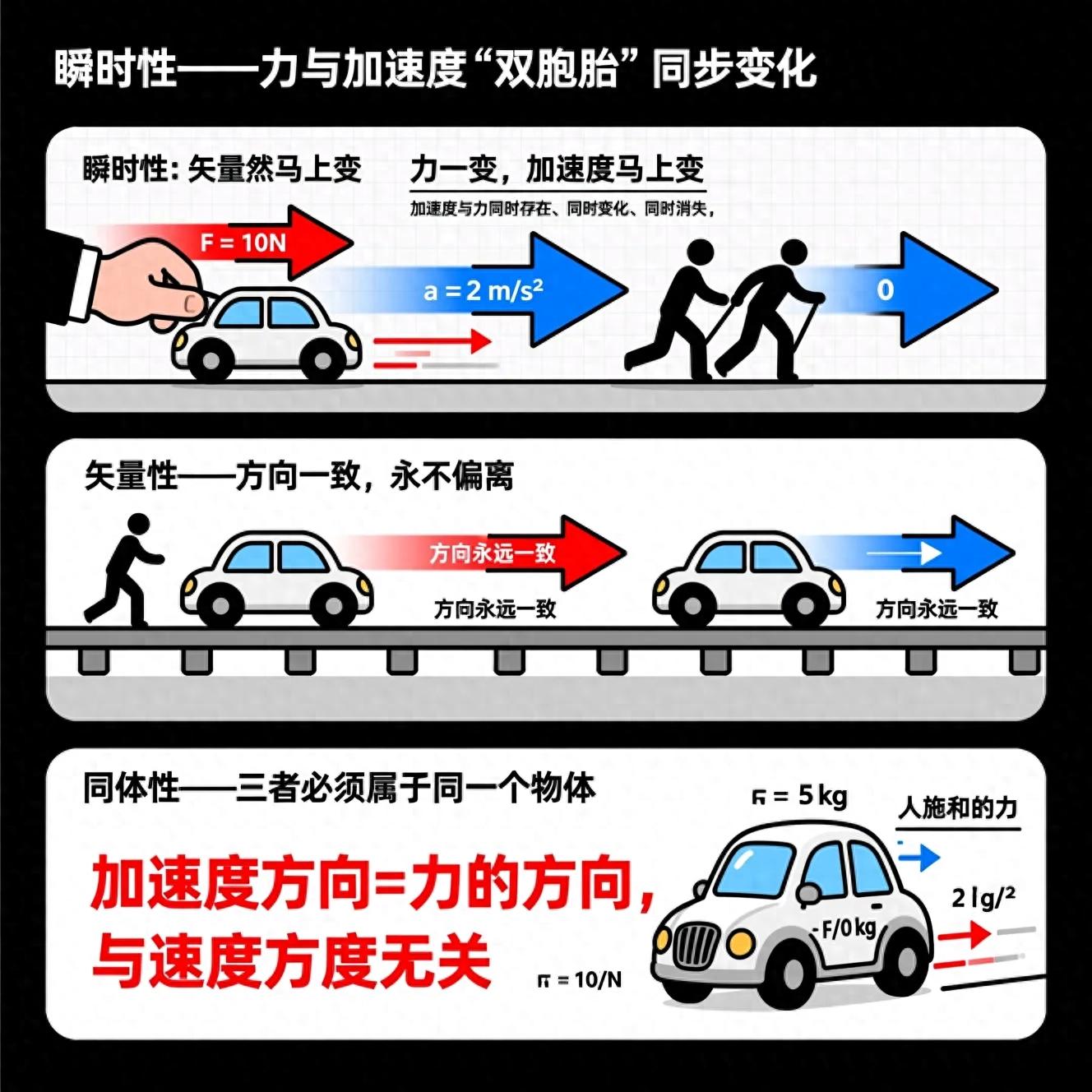
牛顿第二定律揭示了力的即时效应，指出加速度与力的出现、变化以及消逝是同步发生的。

矢量性：是一个矢量表达式，加速度和合力的方向始终保持一致。

物体在多个外力共同作用时，若单独考虑其中一个外力，其导致的加速度仅与该外力相关，不受其他外力影响。各个外力单独作用时产生的加速度的矢量和，恰好等于所有外力共同作用时产生的合加速度，而合加速度的大小和方向则直接取决于合外力的大小和方向。

力的存在导致加速度的产生，而加速度则是力施加后的直接结果，因此，力成为了促使物体运动状态发生改变的根本因素。

等值不等质性：尽管它并非力量，却揭示了物体状态的变化；尽管它仅是衡量物体质量大小的手段kaiyun全站app登录入口，m的数值与物体的体积或形状并无直接关联。

实验验证

牛顿第二定律的实验在物理学领域属于基础且至关重要的验证性研究，它关乎到对某一物理定律或规律的检验途径与方法，因而对该实验的精确度提出了特别的要求。

牛顿第二运动定律的验证实验，主要是通过测量运动系统在不同作用力影响下的加速度，进而验证这些加速度与作用力之间是否满足既定的关联性。

通过运用先进的实验设备对原有的实验方法进行优化与补充，可以更充分地展现物理学科的科学精神与严谨态度。

牛顿第二运动定律主要的实验验证方法

实验验证方法

用打点计时器法验证：

在探讨系统加速度与系统质量及拉力之间的相互关系时，实验中首先将打点计时器稳固地安装在木板的一侧，接着将砝码和小车分别系在细线的两端，细线穿过滑轮，砝码的重量转化为拉力，推动携带纸带的小车在平坦的表面上进行运动。这样，小车、小车上的砝码以及系在细线另一端的钩码共同构成了一个整体的运动系统。

每次实验均须在纸带上注明拉力和系统的质量。

为了克服摩擦力的作用，我们通常采用以下两种技术手段：一是倾斜滑动技术，二是水平拉线技术。

在气垫导轨上验证：

在将气垫导轨调整至水平状态之后——考虑到导轨多少会有些弯曲，导致滑块与导轨之间产生一定的阻力——实验中通常以滑块通过两个光电门时的速度一致作为调平的标准，进而测量出粘性阻尼常数b。

为了纠正由粘滞性摩擦力造成的速度下降，有必要攻克粘滞性阻尼系数的测量难题。这一过程主要采用以下两种技术手段：一是倾斜导轨技术，二是振动测量技术。

用非线性回归法验证：

在气垫导轨实验中，验证定律时测量受空气阻力影响显著，但通过调整方法，这种影响可以被降低至几乎可以忽略不计的水平。然而，通常使用的单一变量线性回归分析并不能充分说明整个回归方程的优劣；而双变量线性回归分析也存在着某些不足。

通过非线性回归技术对定律进行实证，初期需对质点运动的相关动力学模型实施线性化操作，进而获取该模型的参数线性近似数值，随后以此数值作为非线性模型起始点，对动力学模型实施非线性回归分析。此非线性回归技术不仅验证了定律的准确性，还优化了验证定律的常规实验流程，展现出其在应用和推广方面的潜力和价值。

除此之外，还有依托于LabVIEW的教学平台进行牛顿第二运动定律的验证、利用无线模块和Visual Basic进行的仿真演示实验设计、以及采用光电传感器的实验装置。

适用范围

牛顿第二运动定律的适用范围局限于质点。在处理质点系时，我们通常运用隔离法，亦或是采用质点系的牛顿第二定律。

牛顿第二运动定律的适用范围仅限于惯性参考系，即那些牛顿运动定律能够准确描述运动情况的参考系。然而，在非惯性参考系中，牛顿第二运动定律并不适用。不过，通过引入惯性力这一概念，我们可以在非惯性系中依然使用牛顿第二运动定律的表示形式。

牛顿第二定律仅适用于宏观现象。在处理微观问题时，量子力学是不可或缺的。当物体的运动尺度与德布罗意波相当，粒子运动的不确定性原理（即无法精确同时测量粒子的运动方向和速度）导致动量和位置这两个物理量无法同时被精确确定，因此，牛顿动力学方程因缺乏准确的初始条件而无法进行求解。也就是说，传统的描述方式，因粒子运动的不确定性原理而变得不再适用，或者需要作出相应的调整。量子力学中，通过希尔伯特空间中的态矢这一概念，取代了位置和动量（或速度）的描述，即通过波函数来展现物体的状态；同时，它以薛定谔方程取代了牛顿动力学方程，即取代了包含力场具体形式的牛顿第二运动定律。采用态矢来表示位置与动量的原因，是因为测不准原理的限制使得我们无法确切地同时掌握位置和动量的具体数值。尽管如此，我们能够了解到它们各自的概率分布。测不准原理对测量精度的制约，主要体现在这两个概率分布之间存在一种确定性的关联。

牛顿第二定律在低速情境下有效。对于高速运动的情况，则需要借助相对论来处理。牛顿的动力学方程与洛伦兹协变原则不符，因此无法与狭义相对论兼容。这就意味着，在物体高速运动时，必须对力、速度等力学量的定义进行修正kaiyun全站网页版登录，以确保动力学方程符合洛伦兹协变的条件。这样的修正会导致物理预测在速度接近光速时与经典力学产生差异。

发展简史

1662年，伽利略·伽利雷提出观点，指出运动的物体若非受到加速或减速的外力影响，其速度将保持恒定。同时，勒内·笛卡尔也持有类似看法，他认为，在无外力作用的情况下，粒子要么保持匀速运动，要么保持静止状态。

艾萨克·牛顿将此假设确立为牛顿第一运动定律，同时，他对伽利略的理论进行了深化，将其应用于存在显著力作用的场景，并据此提出了牛顿第二运动定律。

自1684年8月起，牛顿在埃德蒙多·哈雷的鼓励下着手撰写《自然哲学的数学原理》，对稿件进行了系统整理，并对某些问题进行了重新思考。到了1685年11月，这部专著已初具两卷规模。随后在1687年7月5日，《原理》以拉丁文形式正式出版。在《原理》的绪论部分，关于运动的公理或定律的章节中，牛顿提出了著名的第二运动定律。

应用领域

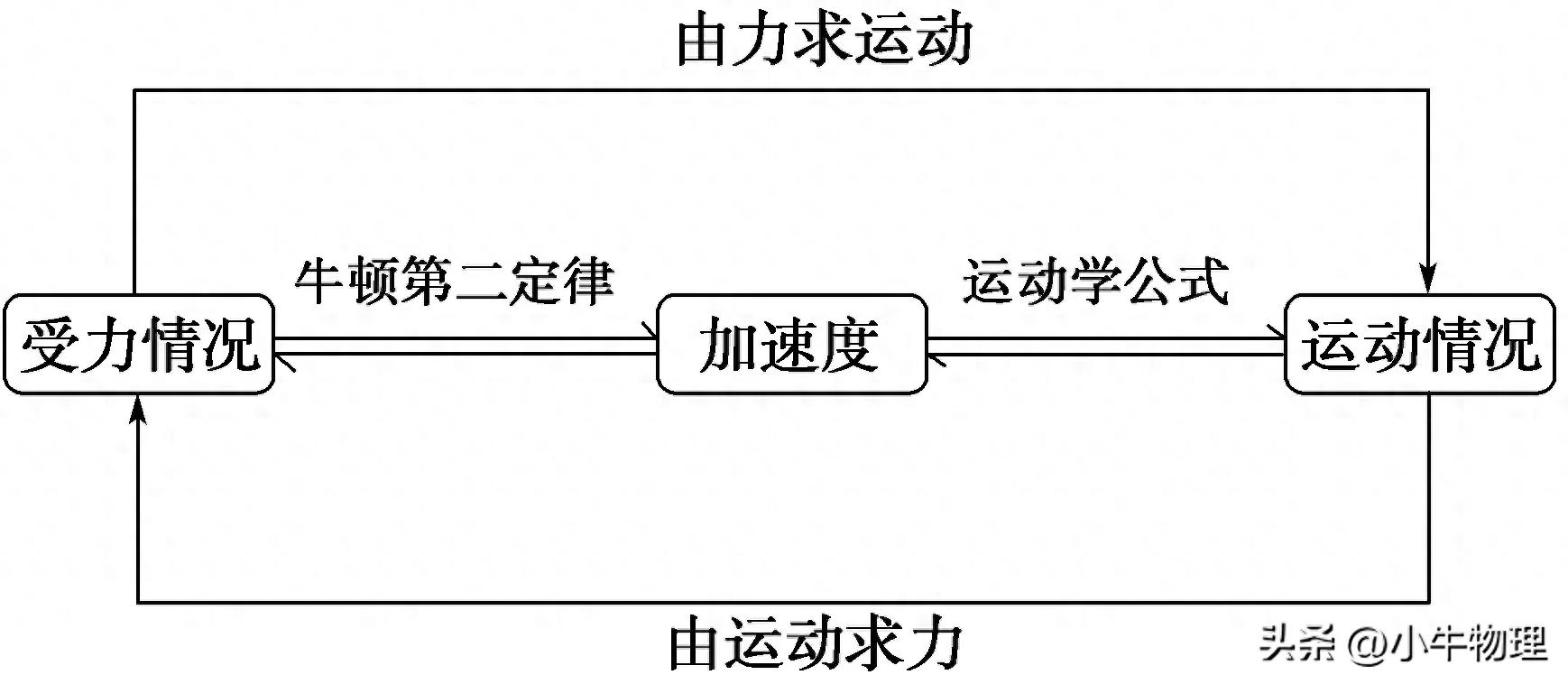
应用牛顿第二运动定律可以解决一部分动力学问题。问题主要分为两大类，首先，对于第一类问题，我们已知质点的质量以及其运动状态kaiyun全站登录网页入口，包括任意时刻的位置、速度或加速度的表达式，我们的任务是求出作用在物体上的力。这通常涉及到对已知的运动方程进行时间上的二阶导数运算，或者对速度方程进行一阶导数运算，从而得到加速度。随后，根据牛顿第二定律，我们可以计算出未知的力。其次，对于第二类问题，我们已知质点的质量以及作用在其上的力，目的是求出质点的运动状态，也就是求出运动方程、速度表达式或加速度表达式。这通常需要依据牛顿第二运动定律列出相应的方程，求出物体的加速度表达式。接着，通过加速度和初始条件，我们进行定积分运算以得到速度表达式，再通过速度表达式和初始条件，进行定积分运算以得到运动方程。解题途径涵盖了以下四种主要方法：首先，临界条件法；其次，正交分解法；再者，合成法；最后，程序法。

依据牛顿第二定律和矢量合成原理，结合“平行导轨模型”的理想物理特性，并遵循电磁感应定律，对电容负载在电磁感应过程中所涉及的平行导轨模型进行详尽计算，从而得出不同情形下金属导杆运动的具体数学公式；这些计算结果与实际观测数据相符。

动画艺术，通过使画面产生动态效果，呈现了一种独特的影视表现形式，亦即动态的画面。在动画领域，牛顿的第二运动定律扮演着至关重要的角色，成为动画研究中的一个不可或缺的核心内容。

定律影响

依据牛顿的第二运动定律，我们确立了国际单位制中力的度量单位——牛顿，其符号为N；该单位指的是能够使质量为1千克的物体获得每秒1米的平方加速度的力；换句话说，1牛顿等于1千克乘以1米每秒的平方。

牛顿第二定律精确地揭示了物体运动状态改变与所受力之间的联系，与牛顿第一定律及第三定律相辅相成，构成了牛顿运动定律体系，在力学领域占据关键地位，并作为经典力学研究的基石，详细阐述了该领域中运动的基本法则。