折叠问题中所包含的勾股定理的运用
中考中,折叠问题既是热门也是难点,它常常与动点问题相互关联。这类问题的设定往往涉及将特定图形按照特定条件进行折叠,解答时需分析折叠前后的图形变化,并利用轴对称特性、勾股定理等知识来求解。
这类问题构思独特,变化多端,要妥善解决它们,不仅需要运用轴对称图形的特性来绘制所需图形,而且还需巧妙地运用各种数学模型与解题技巧。
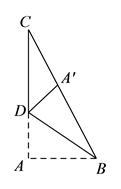
在图1-1所示的直角三角形ABC中,角A的度数为90度,边AB的长度为3,边AC的长度为4。接下来kaiyun.ccm,我们将三角形ABC沿着线段BD进行翻折操作,确保点A能够准确无误地落在边BC上。根据这一翻折过程,我们可以得出线段CD的长度。

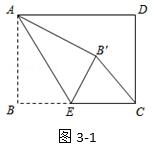
在长方形ABCD中,边AB的长度为3,边BC的长度为4。点E位于边BC上。连接点A和点E。将角B沿着线段AE进行折叠,使得点B与点B'重合。当形成的三角形CEB'为直角三角形时,线段BE的长度是多少?

解题要点在于对问题进行细致的分类分析,然后通过绘制相应的图形,运用折叠特性以及勾股定理来解决问题。
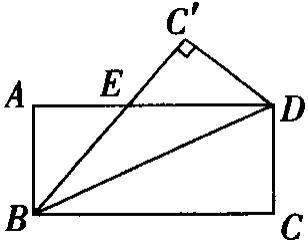
在长方形ABCD中kaiyun全站网页版登录,将边DBC沿着BD这条边进行对折,使其到达新的位置DBC’,此时,边BC’将与AD这条边相交,并在交点处形成点E。
(1)需阐述:等式BE等于等式DE;(2)在AB等于6,BC等于8的条件下,计算三角形EBD的面积。

在矩形ABCD中,边AB的长度为3,边AD的长度为5。按照图示,对纸片进行折叠,确保点A与BC边上的点A'重合,折痕记为PQ。随着点A'在BC边上移动,折痕PQ的端点P和Q也会相应地变动。如果规定点P和点Q必须分别沿着AB边和AD边移动,那么点A'在BC边上能够移动的最远距离是 __________。

这道题目较为复杂,主要侧重于对学生分析及绘图技能的考查。解题时需遵循一个原则,即折叠前后的线段长度保持不变。首先,需要确定点A折叠后的位置A'。接着,依据对称轴(即折痕)作为对应点连线的垂直平分线kaiyun官方网站登录入口,来确定折痕PQ的确切位置。在此过程中,可以运用勾股定理、正方形的判定定理及其相关性质来计算所需的线段长度。