数学世家伯努利家族

伯努利家族是 17 至 18 世纪瑞士的一个非常出名的家族，出过很多数学家，祖籍在比利时安特卫普。这个家族里三位主要人物是雅各布·伯努利、约翰·伯努利和丹尼尔·伯努利，他们做了非常重要的事，他们的证明方式显示出很高的数学创造力，并且对历史产生了很大影响。以下将详细阐述：

雅各布·伯努利是一位著名的数学家，他出生于1654年，逝世于1705年。

核心贡献：概率论、无穷级数、极坐标、伯努利数

概率学开山之作《猜度之艺》，完成于公元一千七百一十三年

2. 调和级数发散性证明

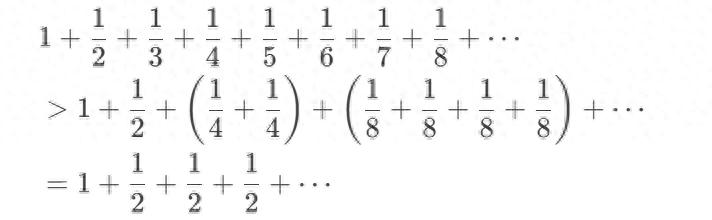
构造发散子级数：每组和为

，无限组故发散。

意义 ：打破当时“级数通项趋于零则收敛”的误解。

伯努利数和伯努利多项式属于数学领域，二、约翰·伯努利是一位著名的数学家，他出生于1667年，逝世于1748年

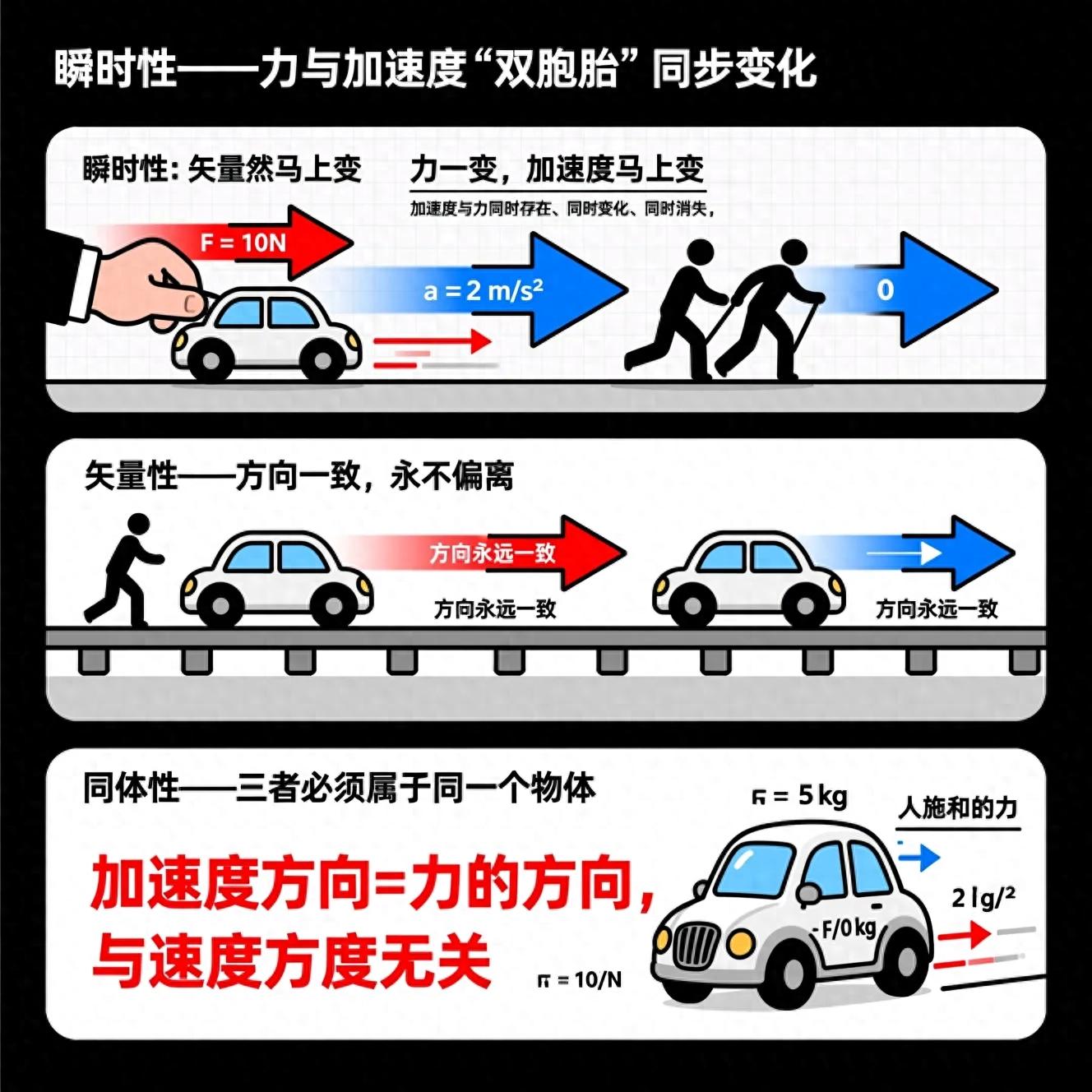
主要功绩在于推动了微积分的演进，首创了变分法这一核心分支，并且攻克了最速降线这一重大难题。

洛必达法则的真正创立者,最速降线问题在1696年提出,指数微积分的主要奠基人,丹尼尔·伯努利生于1700年,卒于1782年

主要成就：在流体力学方面，成果突出；在概率统计方面，见解深刻；在振动理论方面，影响深远。

伯努利原理阐述流体动力学特性，著作发表于1738年；弦振动理论探讨振动弦的规律；概率与效用理论研究不确定情境下的决策选择。

总结：伯努利家族的学术遗产

人物

核心贡献领域

关键成果与证明思想

影响

雅各布

概率论、级数

组合不等式与极限理论可以用来证明大数定律，调和级数通过分组比较的方法可以证明其发散kaiyun官方网站登录入口，伯努利数能够借助生成函数求得

为概率论奠定了坚实基础kaiyun全站登录网页入口，有力推动了组合数学的发展

约翰

微积分、变分法

运用无穷小量替换技巧的洛必达法则，以及借助离散透射模拟方法推演出微分方程的最速降线理论

促进了微积分算法的发展，开创了变分法这一重要领域

丹尼尔

流体力学、数学物理

能量守恒原理可以用来推演出伯努利法则，琴弦的振动规律能够借助微元牛顿法则求出，那个著名的圣彼得堡难题则通过引入对数效用法则加以说明

构建了流体动力学体系，成功导出波动方程kaiyun全站app登录入口，开创了期望效用理论

附：证明中的数学工具演进

伯努利家族的学术探索，完成了从组合方法到微积分研究，再向物理构建的关键转变。他们提出的论证思路周密细致，富有开创性价值，有力地影响了近代数学与物理学的演进格局。