启发式算法在最优化问题求解中的应用与实践

最优化情形常见于社会生产活动中，我们持续探索更高效、更精准的应对策略，以处理此类情形。通常，最优化情形能够转化为数学规划形式，通过搜寻变量在允许范围内的各种搭配kaiyun全站登录网页入口，来获取目标函数的最佳结果。针对常规的最优化情形，存在多种处理手段，例如梯度下降法，以及拉格朗日乘数法等。但是，存在一种最优化难题，人类至今无法攻克，那就是NP完全问题。本文阐述了最优化问题的普遍用途和解决途径，尤其深入探讨了启发式算法在寻找NP难题近似解时的运作机制。运用模拟退火法与蚁群法探寻最优路径的案例，验证了借助启发式方法可获得NP问题的近似最优解kaiyun全站app登录入口，为我们在日常工作中处理这类时间复杂度不明的最优化课题，提供了一种成本经济且目标效率更优的应对策略。

引言

工作运行过程中，常常碰到一些情况：比如，超市的配送车辆要往多个店铺运送商品，怎样安排车辆的送货顺序，才能让每个店铺都能收到商品，同时让车辆行驶时间与路程最省；又比如，某个视频网站要在全国多个地方放置视频存储设备，既要确保这些设备的位置能服务所有客户，还要减少用户与设备之间的网络传输费用，提升视频请求的处理速度，同时也要尽可能少地设置设备，以节省开支；这些路线安排和资源分配的难题，都属于最优解问题解决的范畴。处理最优解问题的技巧称作最优解技巧，惯用的最优解技巧包含若干类型：首先是梯度下移技巧，其次是牛顿式技巧，再次是协同下降技巧，然后是拉格朗日配对技巧，最后是直觉式技巧。这五种技巧各自具备特定的适用条件与独到之处，因此处理最优解问题之时，必须先考察实际情境，再挑选恰当的最优解技巧，这是首要步骤。计算机科学的核心任务包括两个层面，一是找到能够验证其运行效率出色，并且能解决各类问题最优方案或次优方案的算法，二是面对最优化议题时，存在一类挑战人类目前难以攻克的难题，即NP完全问题，这类问题同时也是公认的七大数学难题之一，不过庞加莱猜想已经被俄罗斯数学家格里戈里·佩雷尔曼攻克了NP指的是多项式复杂度上的不确定性难题，所有能在非确定性多项式时间内解决的判定任务都属于NP问题集合。处理这类任务时，传统确定性时间复杂度的方法不再奏效，而启发式这类非确定性时间复杂度的方法，反而能较佳地找出该类问题的一个可接受次优方案。一般情况下，启发式算法在解决问题时，其搜索到的结果并非最佳答案，而是随着算法的优化和重复计算，逐渐趋向于理想解的近似解。由于当前尚未发现一种更优越的算法，这种算法既能在执行效率上表现优异，又能在稳定性方面有可靠保障，并且能够确保获得问题的完美答案，因此，启发式算法成为了我们应对这类挑战的一种较为有效的方法。常见的求解方法包括模拟退火技术、遗传策略、蚂蚁系统以及人工神经网络等。这些方法都无法明确其运算过程的时间复杂度，也无法验证其计算结果是否为最优方案。不过它们通常能在合理的时间内，找到令人满意的解决方案。判定为“尚可”，标准在于确保生产所需的基本时长，判定为“良好”，标准在于找到虽非最佳方案，却能满足生产需要并提升效益的方案，因此钻研启发式算法，对于我们在生产实践中处理某些优化课题具有显著价值。启发式算法近年应用与探索增多，人工神经网络在机器学习方面应用颇广。其余三种启发式算法，均模拟自然界生物现象而设。模拟退火方法借鉴了固体物质冷却的原理，主要应用于组合优化类课题；遗传算法效仿了达尔文生物进化论中的自然选择与遗传机制，旨在应对搜索类课题；蚁群算法则模仿了蚂蚁觅食时探测路径的习性，专注于解决路径优化课题，这类算法颇具趣味性。这项研究着重于三个方面：首先，阐述了最优化问题的基本概念，并探讨了其典型应用情形与处理途径；其次，深入剖析了P类问题、NP类问题以及NP完全问题（即NP-C问题）的特征；再次kaiyun官方网站登录入口，系统介绍了各类启发式算法的原理与应用，尤其对模拟退火算法和蚁群算法这两种代表性启发式方法在处理NP类问题时的具体运用进行了详细说明和实际操作。

常见最优化问题及其解决方法

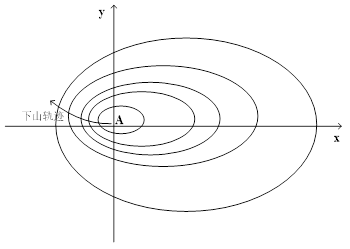
下山的最佳路线选择与梯度下降方法 类似图2.1的描绘，设想存在一座山体，其周边被浓密雾气笼罩，视线无法穿透。从山顶的A位置起步，如何确定一条通往山底端的效率最高路径，便构成一个优化课题。处理这个议题时，我们将该座山视为一个可以进行求导的数学关系，山体的高度作为该关系的特定输出，也就是需要确定一条路线，让该关系的输出数值减少得最为迅速，从而能够探寻到最便捷的下行路线。