基于支持向量机和遗传算法的人脸识别研究
采用自适应遗传算法,优化并筛选高斯核函数支持向量机参数模型,用于人脸特征分类。支持向量机的推广能力关键在于核函数种类、核函数参数以及惩罚因子C的选择,本文在经典高斯核函数上设计了新型高斯核函数,充当支持向量机的非线性转换工具,同时借助自适应遗传算法来寻找核函数参数和支持向量机惩罚因子的最佳组合,最终把调整过的SVM模型应用于人脸数据集开展模拟测试。实验结果显示,本文提出的方法在识别准确率方面超越了传统的高斯核函数支持向量机分类器模型。
0 引言
人脸识别属于模式识别的一个分支,也归属于生物识别范畴,与其它人体生物特征识别手段相比,它具备操作便捷、采集简单、无需接触等多项长处,同时,人脸特征自身具备良好稳定性与显著个体差异,非常适合作为身份核验的参考标准,因此,对人脸识别开展深入研究,既拥有重要的学术探讨意义,也展现出极为宽广的应用潜力。在具体操作中,因为受到多种因素制约,常常难以为每个人收集足够多的照片资料。因此,针对人脸识别这类任务,其本质上属于小样本模式识别的范畴,而支持向量机在处理小样本、非线性以及高维模式识别方面,相较于其他常规分类方法展现出显著的优势,这种优势体现在SVM能够平衡学习效果与泛化性能,既确保了分类结果的准确性,也兼顾了模型的推广能力。所以,这项研究采用支持向量机来识别面部特征,由于这种算法的预测能力与其核函数种类、核函数的调节因子以及惩罚参数密切相关,参考了众多学术资料,研究者在效果更优的高斯径向基函数(RBF)上,开发了一种改良的高斯函数,并将其作为支持向量机的非线性转换工具。寻求更佳的SVM分类器模型效果,运用自适应遗传算法来调整其参数,随后将调整后的SVM分类器模型应用于人脸数据库开展实验验证。实验结果显示,本文提出的方法相较于传统的高斯核函数支持向量机模型,展现出更高的识别准确度。
1 支持向量机模型
1.1 支持向量机概述

如图1所示,SVM技术可以处理一组非线性可分的高维数据,如图(a)所示,通过核函数将其转换到更高维的特征空间,使其变为线性可分,如图(b)所示。(b)图中H是能够有效区分两类数据点的最大分隔超平面,H1和H2是与H平行的两个超平面,它们分别穿过距离H最近的两类数据点,位于H1和H2上的数据点被称为支持向量,超平面的数学公式见公式(1)
公式里kaiyun全站网页版登录,xi代表一个输入数据,yi表明这个数据属于哪个类别,核函数用?鬃表示,支持向量集记为SV,分类边界值是b*,每个数据点的拉格朗日乘子记作?琢i,符号函数用sgn来表示。
1.2 核函数选取
现有核函数类型主要有四种:线性型、多项式型、S曲线型和高斯径向基函数,其中后者即径向基函数,应用最为广泛,本文基于此提出新型高斯函数,将其作为支持向量机的非线性转换工具,该新型函数能够克服传统高斯函数的两个关键缺陷:一是测试点附近函数值衰减缓慢的问题,二是远离测试点时函数值趋近于零导致的核函数截断效应。现有研究明确,高斯函数存在两个主要不足,这些不足会在一定程度上削弱分类能力。本研究将针对人脸识别任务,对高斯函数进行优化,以此检验其应用效果,并对比传统高斯函数的优势。
高斯核函数表达式如下:
其中,xc为测试点,
是核带宽变量。
高斯径向基核函数图像如图2所示。
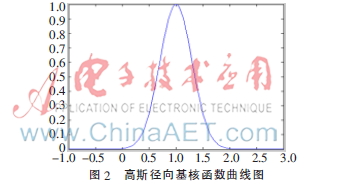
改进高斯核函数表达式如下:
式中,xc是测试点,?滓是核带宽变量,p是位移参数。
本文将高斯核函数和改进高斯核函数的偏置系数均设定为0.3,改进高斯核函数的指数参数确定为0.2,通过实验对这两种核函数进行对照分析,图3展示了它们在测试点附近的衰减行为差异,图4则呈现了它们在远离测试点时的衰减速率对比。
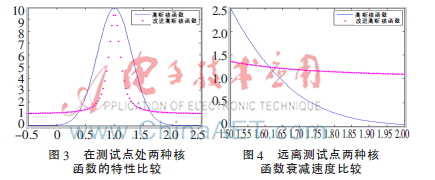
根据图3和图4可知,本文提出的改良高斯核函数能够有效克服高斯核函数的两个主要不足之处,具体表现为在测试点附近具有更快的衰减速率,而在远离测试点时其衰减速率又显著低于传统高斯核函数,从而避免迅速接近零值,因此将该改良高斯核函数应用于非线性分类任务时,能够充分展现其低误判率的优势。
2 遗传算法优化SVM参数模型
2.1 遗传算法
本文运用自适应遗传算法来优化筛选SVM参数,这种算法可以针对搜索阶段某个特定解给出最优的交叉率与变异率,算法里的交叉率Pc和变异率Pm通过以下公式确定:
那个,favg指的是整个集体的适应度平均值,fmax则表示集体中适应度最高的值,f是参与杂交的两个个体里适应度较大的那个,f ′代表经过变异操作后个体的适应度,而k1、k2、k3、k4是一些固定的系数。
自适应遗传算法里的挑选方式运用了赌轮机制,适应度函数的制定方式是,
2.2 遗传算法优化SVM参数模型
改进高斯核函数SVM模型包含3个参数,分别为核函数带宽变量
核函数位移参数p和惩罚系数C是关键因素,为了寻得最佳分类器模型,运用自适应遗传算法进行参数的优化选择,具体优化过程包括以下环节:
生成指定数量的初始种群,明确各变量取值区间和编码长度,为每个个体实施二进制编码。
依据公式六确定每个体的适配程度,审视其是否达标,倘若达标,则显示最优体及其体现的极值,并终止运算,若未达标,则进入下个环节。
挑选能够繁殖的个体时,要参考它们的优劣程度,表现更出色的个体获得更多繁殖机会,表现较差的个体则面临被淘汰的风险。
(4)根据交叉概率执行交叉操作生成新个体。
(5)根据变异概率执行变异操作产生新个体。
(6)由交叉和变异产生新一代的种群,返回到第(2)步。
3 实验仿真
本文选用人脸数据库ORL作为实验数据基础,从里面随机挑选了20个人的图像参与实验,把每个人的前5张图像当作训练数据,后5张图像当作测试数据,利用PCA提取的特征进行分类,分别使用改进型高斯核函数SVM分类器模型和普通高斯核函数SVM分类器模型来执行分类识别任务。实验时,自适应遗传算法的参数设定如下:初始种群规模确定为三十个个体,循环次数设定为二十次,因为实践证明这种遗传方法收敛效率较高,所以无需设定过多的迭代周期,k1参数值为0.5,k2参数值为0.9,k3参数值为0.02,k4参数值为0.05,目标函数的精确度要求达到0.0001,常数C和变量p的精确度要求均为0.01,常数C的取值区间为0到500,目标函数的取值区间为0到1,变量p的取值区间为0到50。实验数据如下:
通过反复测试,确定了最优的PCA维度,并设定了优化高斯核函数SVM模型的参数值,具体数值为:核参数设置为0.73082,多项式指数设为30.2649,惩罚系数调整为364.416,随后针对20位被试的后100张图像,采用不同维度的PCA特征进行了10次识别实验,最终计算平均结果kaiyun官方网站登录入口,绘制出图5所展示的关系曲线。
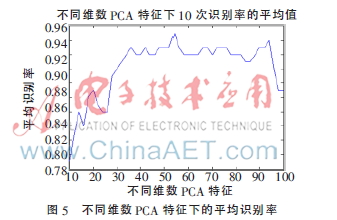
实验数据表明,维度为54的PCA特征最为理想,因此本研究将此特征作为主要识别依据,并继续开展后续研究工作。
采用(1)里设定的参数,运用优化后的高斯核SVM方法执行人脸识别任务,获得准确辨认和识别失误的图像,分别展示在图6和图7中。

采用自适应遗传算法对高斯核函数SVM分类器模型进行优化改良后,在人脸识别任务上的成效,其数据展示于表1。
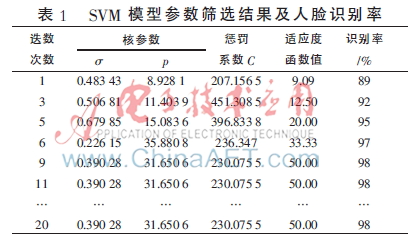
实验结果显示,采用自适应遗传算法优化支持向量机参数的分类器模型,其识别效果相当不错,同时收敛表现也令人满意。
经过反复验证发现,高斯核函数支持向量机模型里,惩罚因子C的大小对分类效果作用不大,但松弛变量在0到12之间取数时,对分类器的表现有显著影响,并且最佳识别准确率也出现在这个数值区间,本项研究将C设为95,并制作了松弛变量在0到12范围内取不同数值时对应的识别准确率变化曲线,如图8所示。
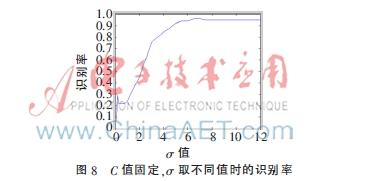
根据图8的信息,若C值保持不变,那么在0到12这个区间内,人脸识别的准确度会随着σ数值的增加而逐步上升。一旦σ超过7,识别的精确度便会稳定在95%左右。
将高斯核函数SVM模型的参数C限定在0到100之间,将σ限定在0到10之间
采用自适应遗传算法调整其参数,调整完毕的分类器模型用于进行人脸识别,识别效果与表1中的识别率进行对照,对照情况展示在表2。
测试结果显示,经过优化的高斯核SVM方案,其判定准确度超过了常规的高斯核SVM方案。
4 结束语
本文着眼于传统高斯核函数存在的两个主要缺陷,研发了一种改进型高斯核函数,该函数能够有效弥补原有核函数的不足,并充当支持向量机的非线性映射工具,同时借助自适应遗传算法对改进核函数的参数以及支持向量机的惩罚因子C进行优化选择,将优化后的支持向量机模型应用于ORL人脸库开展仿真实验,实验结果显示,该模型的分类效果显著优于采用高斯核函数的支持向量机分类器。本方法存在局限性,其稳定性与普适性有待提升,仅在ORL人脸库中包含20人共200张图像的小规模测试中表现出色,当应用于整个ORL人脸库40人共400张图像的模拟识别时kaiyun全站app登录入口,效果并不理想,因此后续研究将聚焦于人脸图像特征的深度挖掘,同时优化SVM核函数及其参数配置,旨在强化分类器的稳定性和适用范围,并进一步提升人脸识别的准确度。




