炒股背后的数学——斐波那契数列,判断市场变盘相对有效!
斐波那契数列,亦称黄金分割数列,源自数学家列昂纳多·斐波那契以兔子繁殖为案例所创,因而得名“兔子数列”。该数列包括:1、1、2、3、5、8、13、21、34、……等等。在数学领域,斐波那契数列通过递推方式定义,具体为:F(1)=1,F(2)=1,F(3)=2,F(n)=F(n-1)+F(n-2)(其中n大于等于4,n属于自然数集)。此外,斐波那契数列在物理、准晶体结构、化学等多个领域均有实际应用。鉴于此,美国数学会自1963年起发行了一本名为《斐波纳契数列季刊》的数学期刊开元棋官方正版下载,旨在专门发表相关领域的研究成果。
斐波那契数列的使用原则:
股市若遭遇重大变故kaiyun.ccm,斐波那契数列便需从零重新累计;否则,则从一数起,并关注次日、第三日、第五日以及第八日的变动。这些数字构成了重要的转折点,对未来走势具有决定性的影响。
斐波那契数列的间隔周期持续增长,导致其所体现的事件影响力逐渐减弱,预测的灵敏度也随之降低。因此,通常人们只关注第34或55个数字,之后的影响将变得微乎其微。
通常情况下,人们会将第13天设定为新一轮周期的起始日,通常即便日后发生重大事件,它们也往往会与周期中的某一天相吻合。
若在多个起始事件的基础上进行推演,连续数日仍无法确定结果时,通常倾向于选择较早的那一天作为参考。
斐波那契数列呈现出横向的周期性,与之相对kaiyun全站网页版登录,黄金分割线则体现为纵向的周期性,这两者结合起来进行分析。以突破压力位的那一日为新的起点,标记为1,并持续关注随后的走势,是平稳上升还是再次突破。
6、可以与其它数列结合使用,但优先考虑斐波拉契数列。
斐波那契数列的实战应用:
实战案例1
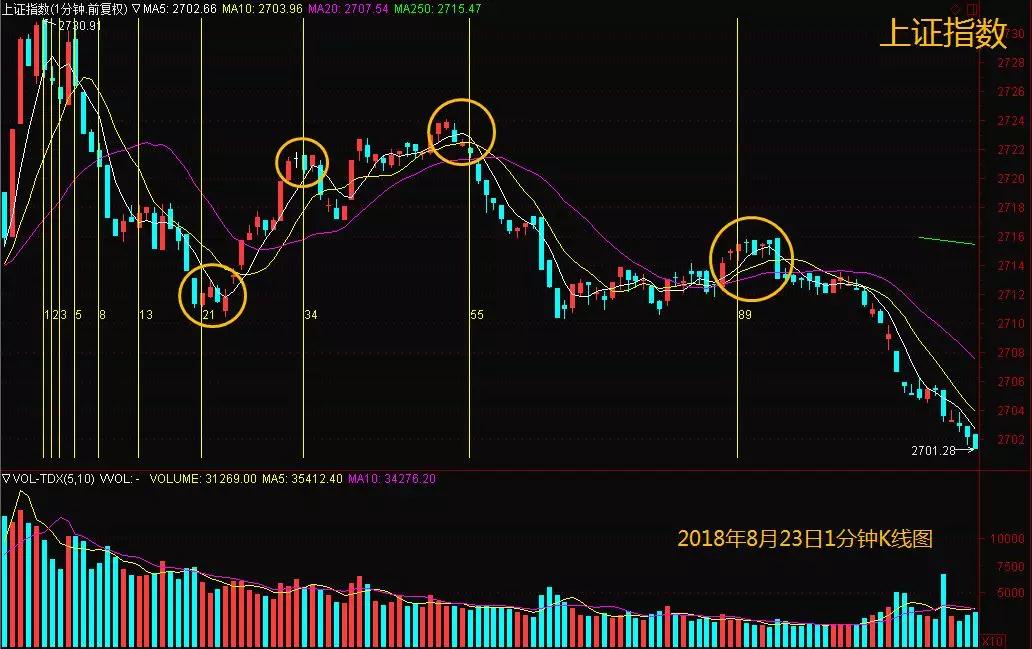
在2018年8月23日的沪指1分钟K线图中,指数经历了四个关键点的转折或变化,这些节点分别是21、34、55和89。

实战案例2
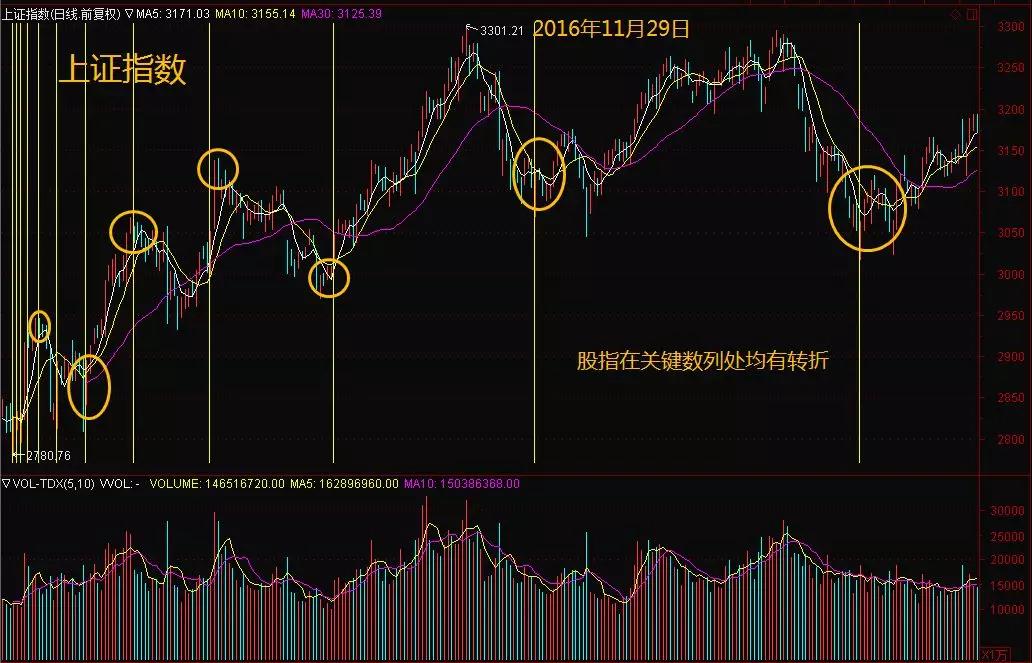
在2016年11月29日,沪指日K图创下新高,其股指在几个关键节点发生了转折,具体表现为:,
实战案例3
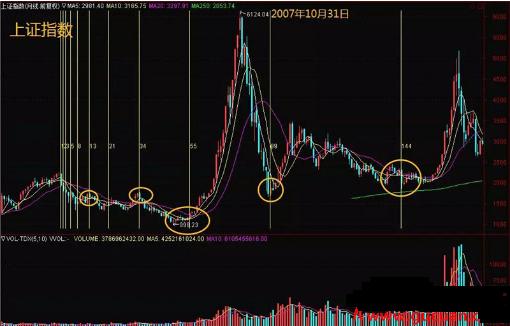
在2007年10月31日创下历史最高点的沪指月度K线图上,我们可以观察到股指在若干关键时点的转折或波动情况,具体表现如下:
实战案例4
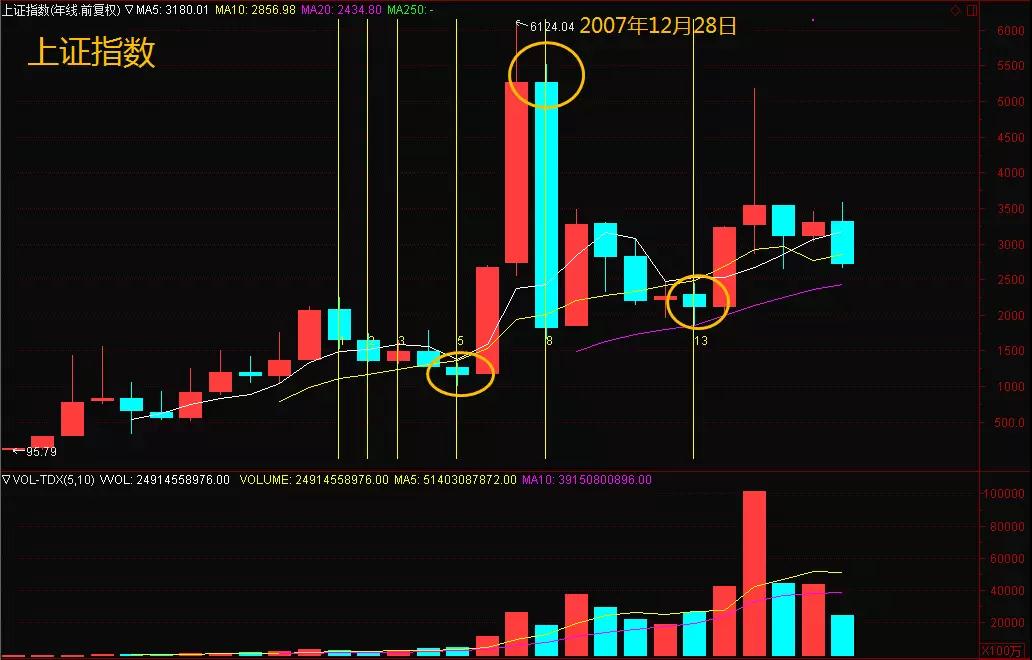
在2007年12月28日创下历史最高点的沪指年K线图中,我们可以观察到股指在若干关键时点的转折与波动情况,具体表现如下: