斐波那契数列,数学界中神一样的存在
你是否曾思考过,为何自然界中某些事物显得如此迷人且协调?又为何某些艺术作品只需一瞥便能触动我们的心弦,激发情感?实际上,这些问题的解答都与一个令人称奇的数学规律紧密相连,那就是斐波那契数列。

斐波那契数列,这一概念最早由意大利数学家莱昂纳多·斐波那契在1202年所著的《算盘书》中提出。他引入此数列,旨在阐述兔子种群数量的增长规律。他设想了一对刚出生的兔子,它们在第一个月便成熟,随后每月都会繁殖出一对新兔子,而这些新兔子在成长后,也会遵循相同的周期进行繁衍。按照这种规律,以此类推,在之后的每个月中各有多少只兔子呢?
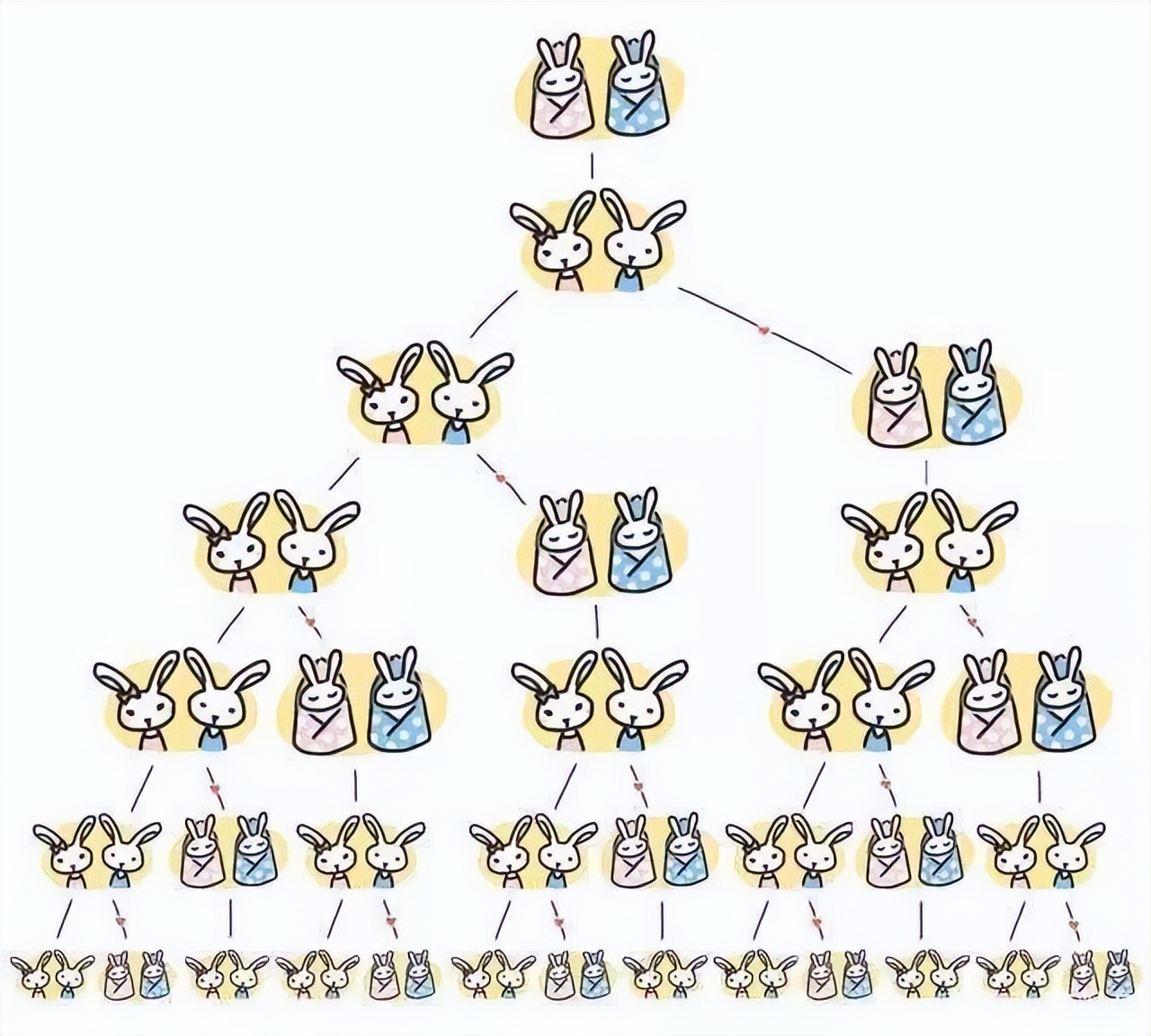
其结果就会形成以下数列:
斐波那契数列中的数依次为1,1,2,3,5,8,13,21,34,55,89,……
观察可知,自第三项起,每一项均等于前两项的相加。这便是斐波那契数列的明确界定:,
F(1) = F(2) = 1
函数F(n)等于F(n-1)与F(n-2)之和,前提是n大于等于3。
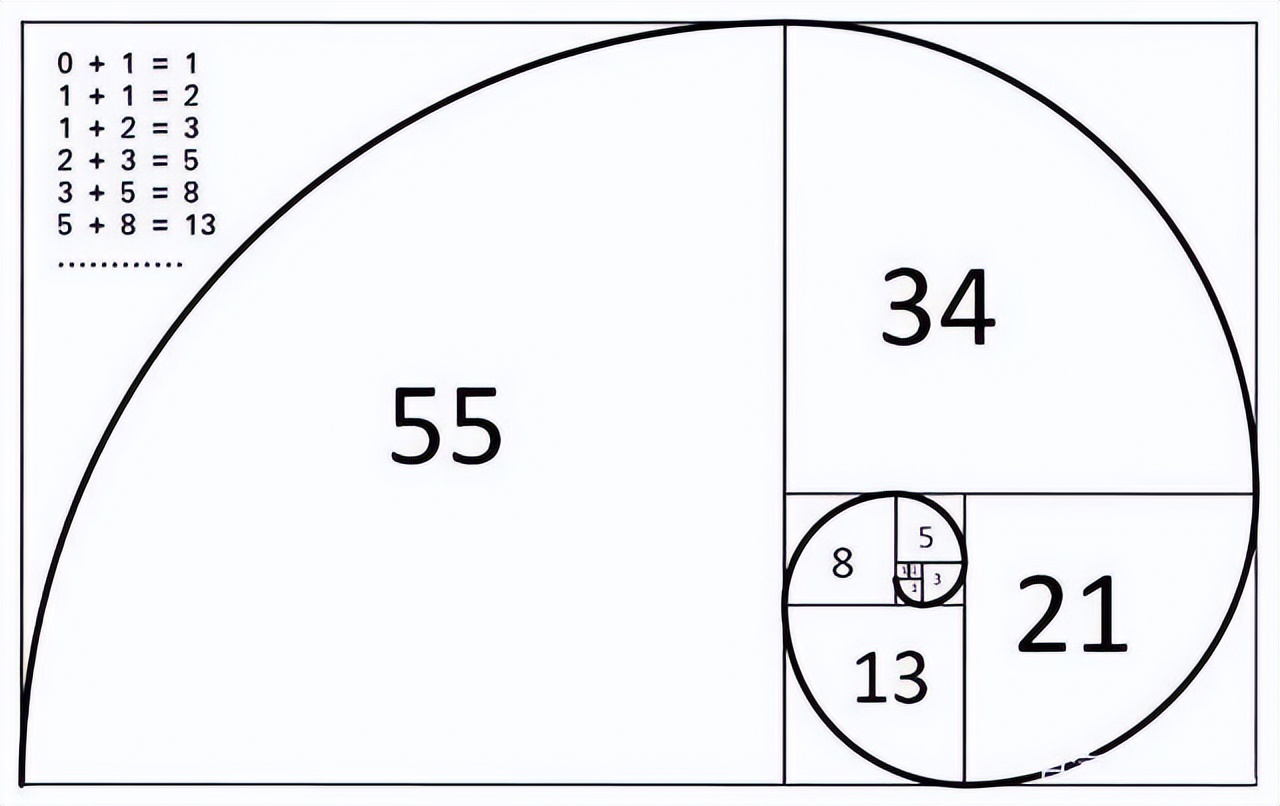
这个数列看似简单,实则深藏无尽奥秘。它与自然界诸多现象紧密相连,同时在艺术、科学和工程等多个领域扮演着关键角色。若您对此存疑kaiyun全站网页版登录,不妨跟随我们一起探索斐波那契数列那令人叹为观止的魅力所在。
斐波那契数列与黄金分割之间存在着一种奇妙的关系。大家应该都知道,黄金分割涉及将一个整体划分为两个部分,这两个部分之间的比例恰好等于它们各自的比例。这个比例大约是1.618,被誉为最和谐的比例,通常称作黄金比例。若我们对斐波那契数列中的任意两项进行除法运算,随着数列项数的持续增加,得到的商数会逐渐趋向于黄金比例。以实例来说明,比如:
F(2) / F(1) = 1 / 1 = 1
F(3) / F(2) = 2 / 1 = 2
F(4) / F(3) = 3 / 2 = 1.5
F(5) / F(4) = 5 / 3 = 1.666…
F(6) / F(5) = 8 / 5 = 1.6
F(7) / F(6) = 13 / 8 = 1.625
F(12)除以F(11)等于144除以89,其结果为1.6179……
这表明斐波那契数列之中蕴含着黄金分割的法则。黄金分割法则在自然界中普遍存在,从植物到动物,从人体到星系,无不显现其踪迹。比如,众多植物的花瓣、种子、叶片等特征都体现了斐波那契数列中的数字,诸如向日葵、菊花、松果、菠萝等。这些植物正是通过这样的方式,来优化空间与光照的利用,从而实现生存与繁衍的目标。

自然,动物界同样适用,比如蜜蜂的家族谱系便依照斐波那契数列排列。蜜蜂分为雄蜂和雌蜂两种。雄蜂仅有一位母亲,并无父亲,这是由于它们是由未受精的卵发育而来;而雌蜂则拥有父母双方,因为它们是由受精卵所孵化。追溯一只蜜蜂的家族谱系,我们会发现开yun体育app官网网页登录入口,它拥有一位母亲,两位祖父母,三位曾祖父母,五位高祖父母,以及八位天祖父母……这些连续的数字,正是斐波那契数列中的那些著名数值。

实际上,人体内存在诸多部位与黄金分割比和斐波那契数列相吻合,诸如身高与肚脐间距离的比例、手指关节与手指长度的比例、五官分布与面部尺寸的比例等。这些比例的存在,使得人体显得更为和谐与优雅。
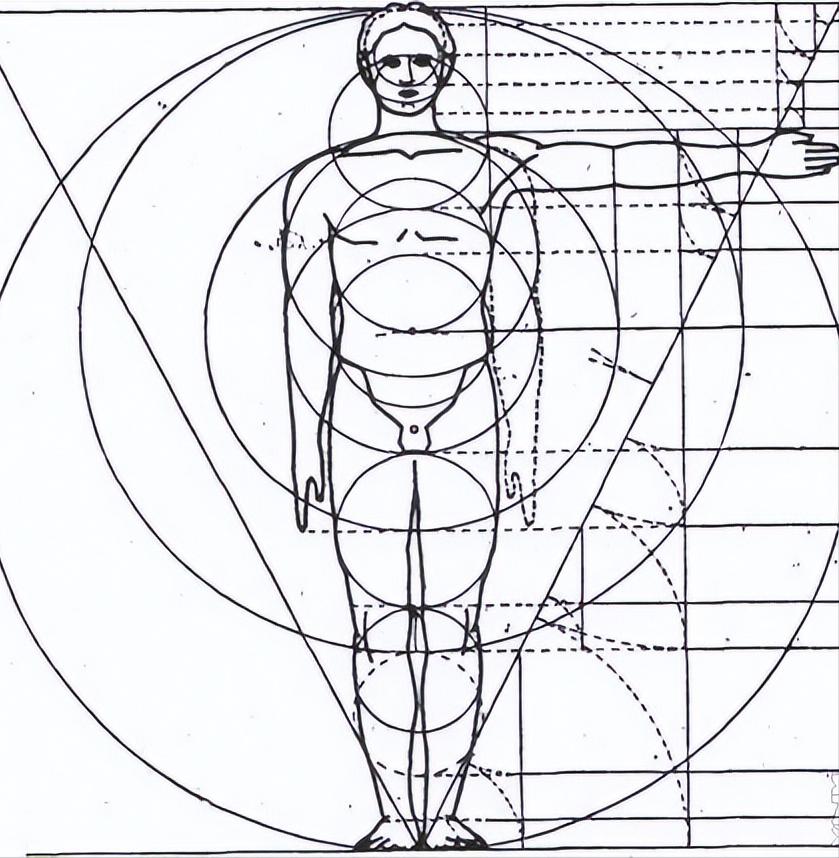
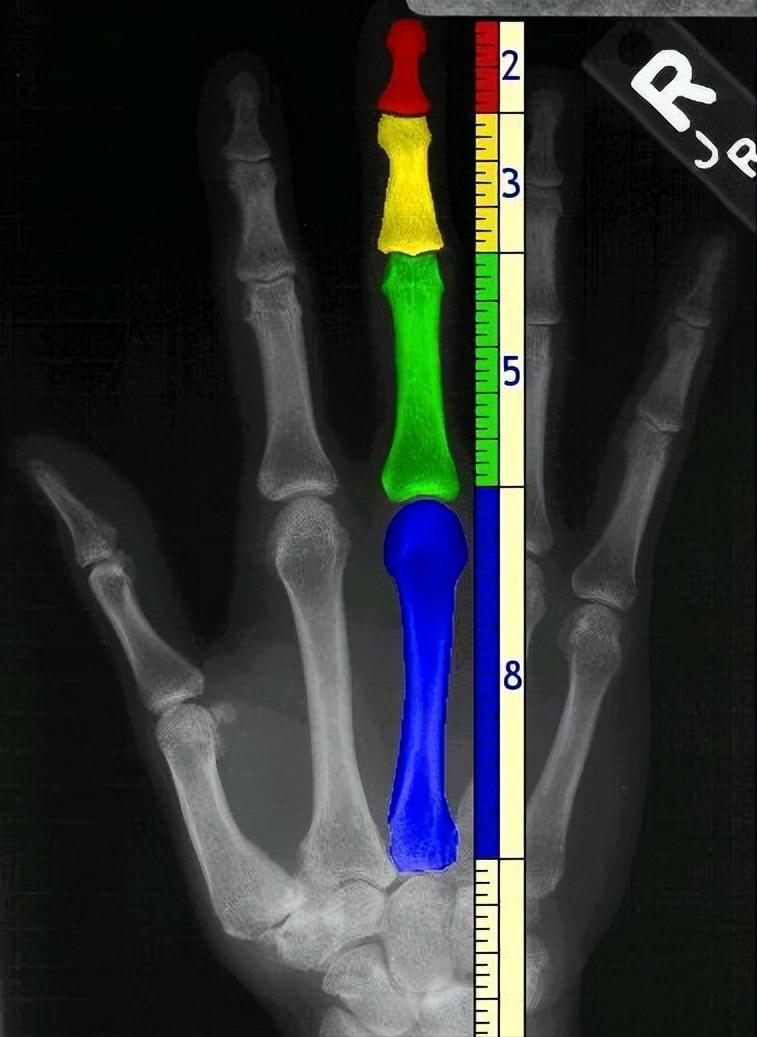
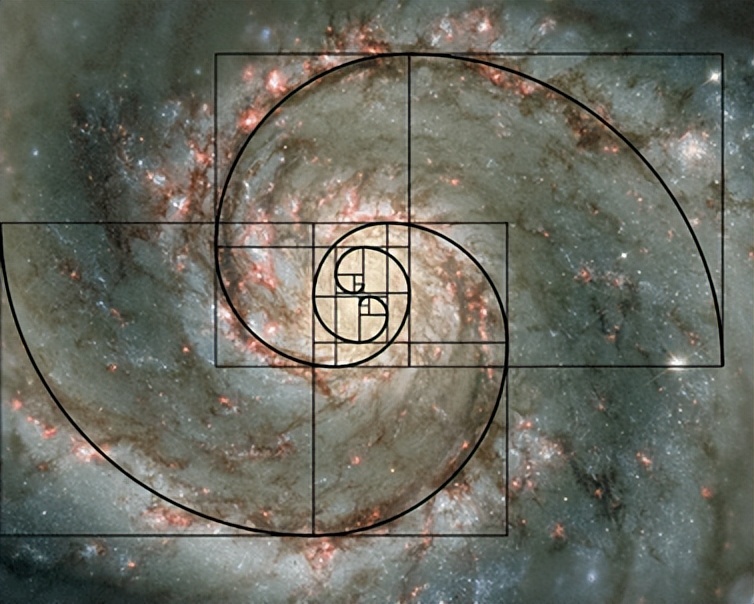
即便是在遥远的星系之中,斐波那契数列和黄金分割的规律依然适用。以银河系为例,其中的旋臂便呈现出一种黄金分割的螺旋形态,这种现象或许与星系的旋转运动以及引力作用密切相关。
斐波那契数列不仅与黄金分割紧密相连,而且在艺术、科学以及工程等多个领域扮演着关键角色。众多艺术家与设计师在创作过程中,采纳了斐波那契数列和黄金分割原理,以创造出既美观又和谐的佳作。以达芬奇为例,他的杰作《最后的晚餐》和《蒙娜丽莎》均采纳了黄金分割的比例,从而使得画面显得更为均衡且富有吸引力。

建筑设计的领域亦然,以古希腊的帕特农神庙、埃及的吉萨金字塔、法国的卢浮宫为例,这些著名建筑均巧妙地运用了黄金分割与斐波那契数列kaiyun全站登录网页入口,从而塑造出既美观又稳固的结构。

音乐创作领域亦不例外,以贝多芬的第五交响曲为例,其中便巧妙地运用了斐波那契数列来规划各乐章的时长与节奏,从而使得音乐作品更加悦耳动听,节奏感也更加丰富多变。
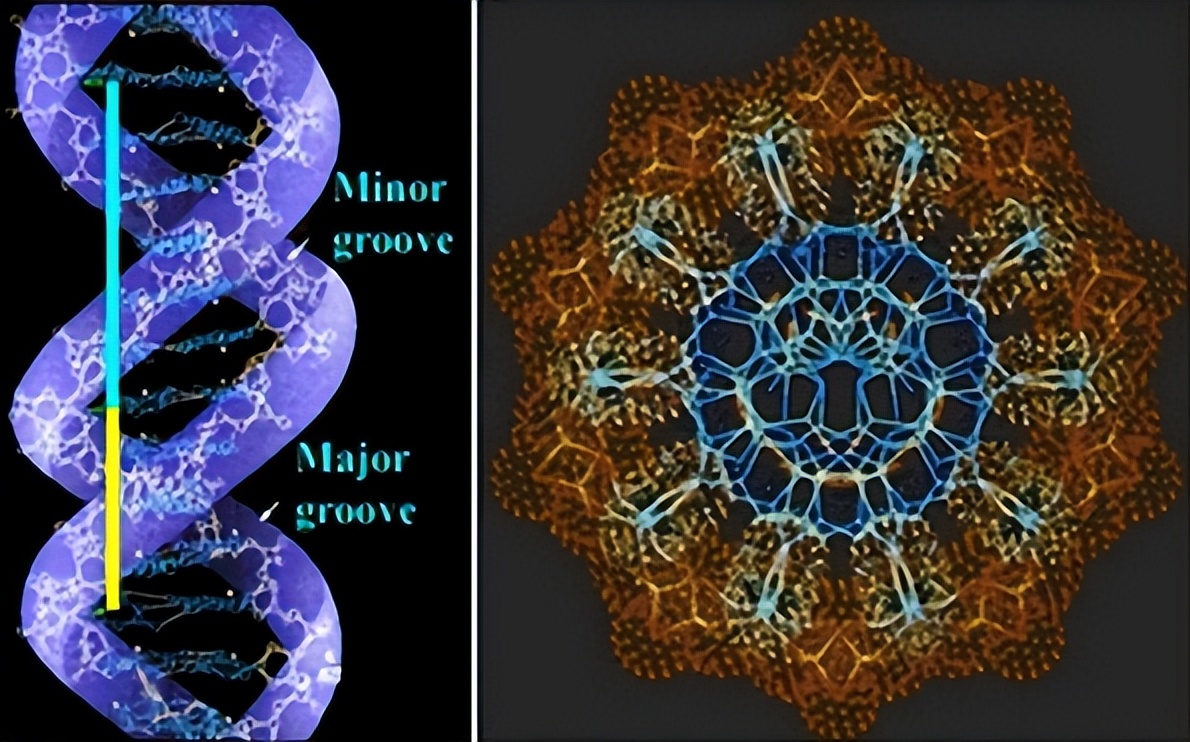
科学界广泛运用斐波那契数列,比如在计算机科学领域,它被用于构建高效的算法与数据结构,诸如斐波那契搜索算法、斐波那契堆等。而在物理学领域,斐波那契数列则有助于阐释某些复杂现象,例如量子力学中的费米子,以及光学中的菲涅尔反射等现象。在生物学领域,斐波那契数列同样适用于阐释某些基因及进化法则,例如,在DNA分子结构中碱基对的排列,以及人类家族谱系中祖先成员的数量。
观察上述实例,斐波那契数列显现出其强大且广泛的数学应用价值,它不仅有助于我们洞察自然界的和谐与规律,还能激发我们创作出卓越且富有价值的成果。此数列让我们领略了数学的韵味,同时也对自然的力量和人类的创造力感到由衷的赞叹。
为何斐波那契数列在自然界中如此普遍?这其中是否蕴含着某种深奥的原理或规律?这无疑是一个相当棘手的问题,同时也极具探究价值。有人认为,斐波那契数列之所以在自然界中广泛存在,是因为它具备最优或最经济的特性,能够帮助生物或物体实现最佳适应性和效率。也有观点指出,斐波那契数列之所以能赋予自然界生物或物体以统一和协调之美,是由于其自相似或递归的性质。而另一些观点则认为,斐波那契数列的随机或混沌属性,使得自然界中的生物或物体展现出多样和变化的魅力。

然而,不论怎样诠释,都无法完全揭示斐波那契数列的神秘与神奇。或许,斐波那契数列是宇宙所藏匿的一把密码,其中蕴含着诸多尚未被我们揭晓的秘密与奇妙。或许,斐波那契数列是自然界的一种语言,它传达着诸多我们尚未领悟的意义与价值。



