斐波那契数列
[id_271324403]
斐波那契数列是这样的数列:
0、1、1、2、3、5, 8、13、21、34 ……
下一项是上两项的和。
例子:下一项是 21+34 = 55
就是这么简单!
长一点的斐波那契数列:
这些数字依次为:0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765、10946、17711、28657、46368、75025、121393、196418、317811……
你可以计算后面几项吗?
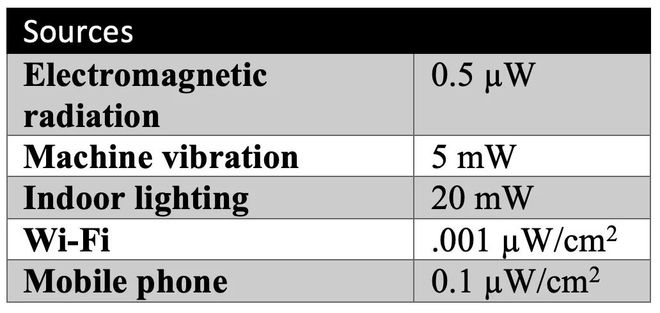
做个螺旋
用这些数作为边长来画正方形,就得到漂亮的螺旋图象:
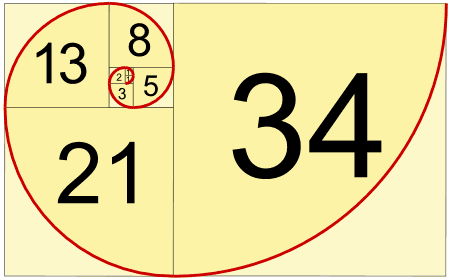
留意正方形整齐地形成螺旋形。
例如,5 和 8 是 13、8 和 13 是 21 等等。
规律
斐波那契数列可以用一个 "规律" 来表达(见数列与级数)。
我们先把项从 0 开始排列:
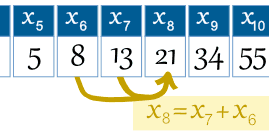
第 6 项的符号是 x6 (等于 8)。
例子:第8项是
第7项加第6项:
x8 = x7 + x6
所以可以这样写成规律:
规律是 xn = xn-1 + xn-2
其中:
黄金比例
令人称奇的是,连续的两个斐波那契数之间的比值,极其接近于著名的黄金比例"φ",其数值约为1.618034……
两个连续的斐波那契数越大,它们的比就越接近黄金比例:
1.5
1.666666666……
1.6
1.625
……
1.618055556……
1.618025751……
……
留意:任取两个正整数作为数列的开端,此规律依然适用。比如,我们可以选取192和16作为数列的起始值:192、16、208、224、432、656、1088、1744、2832、4576、7408、11984、19392、31376……。
0.08333333……
13
1.07692308……
1.92857143……
……
1.61771058……
1.61815754……
……
即便需要更多的条件才能达到优异的比较效果,这仍表明并非只有斐波那契数列才具备这样的特性!
用黄金比例来计算斐波那契数
更奇妙的是,我们可以用黄金比例来计算任何斐波那契数:
答案一定是个正整数,刚好等于上两项的和。
例子:
使用计算器进行计算(仅将黄金比例保留至六位小数),得出的结果为8.00000033。若进行更精确的计算,所得数值将更贴近8。
自己去试试看!
趣事
1/89的结果是0.011235955056179775……,这个数字是一个无限循环小数。
关注前几位数字(如0、1、1、2、3、5)即可识别出斐波那契数列。
实际上,每一个小数点后的数字都存在,然而对于包含多个数位的数字(如13、21等),它们会形成重叠kaiyun全站登录网页入口,具体情形如下:
0.0
0.01
0.001
0.0002
0.00003
0.000005
0.0000008
0.00000013
0.000000021
…… 等等 ……
0.011235955056179775……这一数字等同于分数1除以89。
小于零
数列在零以下也一样:
(自己来算算kaiyun全站网页版登录,看看每项是不是上两项的和!)
在负数范围内,斐波那契数列的求和与正数范围内并无二致,然而其正负符号遵循着正负交替的规则。其计算公式可以表述为:
x−n = (−1)n+1 xn
换言之,第 "n" 项的计算公式为负一乘以 "n" 加一,而 "(-1)" 的指数加一的序列依次呈现为 1、-1、1、-1……的循环。
历史
斐波那契并非首位揭示此数列之人,实际上,在很久以前,印度就已经对这一数列有所了解。

斐波那契
列奧纳多,这位以斐波那契著称的学者,其本名为比萨的列奧纳多,他在1170年至1250年间的意大利度过了一生。
"斐波那契" 是别名,意思是 "波那契的儿子"。
斐波那契不仅传播了斐波那契数列,还大力推广了阿拉伯数字系统开yun体育app官网网页登录入口,这包括我们日常使用的0至9这些数字,用以替换罗马数字体系中的I、II、III等符号。采用这种方式,书写数字变得异常简便。感谢列奧纳多。

斐波那契日
11月23日被称作斐波那契日,缘于“1,1,2,3”正是斐波那契数列的前几个数字。这一天,别忘了提醒你的朋友们哦!