🌾kiayun手机版登录云手机版登录(官方)网站/网页版2025最新版本V4.20

探索写作灵感吗？中文期刊网特意搜集了数学思维在现实生活中的体现，愿为您的阅读和写作提供启发，诚邀大家阅读并传播。 当前数学教育正从多种视角推进，特别是在思想方法层面，不能仅停留在理论层面，要注重实际应用，这种学习方式的优势在于，有助于增强学生的知识运用能力及个人综合素养，为后续学习打下良好基础。数学思维在现...

三个犹太人凑在一块儿，就能左右全局向来有“全球首屈一指的生意人”的叫法统计表明，全球财富雄厚的企业家中，犹太裔占了半数以上美国众多富裕家族里，犹太血统者占了四成之高很多人纳闷，究竟是什么造就了犹太人这般令人咋舌的建树犹太人的典籍《塔木德》中有记述，每个犹太裔的青少年在发育期间，都会面临一个询问。 假如有一天你...

一条铁路线路，连接了二十年的环境巨变；一个交通站点，见证了一个城市的记忆更新。九月二十八日开元棋官方正版下载，“城市历史·展望前景”郑州地铁数字艺术影像展在郑州地铁一号线的绿城广场站入口正式开幕。展览结合过去的画面和数字科技，用人工智能技术构建出穿越时空的桥梁，让乘客能够身临其境地感受郑州从“绿色家园”到生态...

数学思维如何在生活中应用？ 今日聆听了万维刚先生的讲座，方知日常诸多困惑实为数学题解kaiyun官方网站登录入口，与其任由命运摆布，不如钻研数学逻辑，以便危急关头能做出英明决断。 我们日常与人沟通时，常常借助俗语或励志话语，然而这些内容并置，有时会产生冲突。 金岳霖这位逻辑学家，很早就意识到“钱财如同秽物”和...

一位负责发行事务的商人来到出版社，找到我，希望我帮忙编辑他的书，发行部门的负责人便安排我去向这位商人说明书籍的推广点，但我话还没说几句，这位年轻气盛的商人由于没弄明白我是编辑身份，误以为我是发行部门的工作人员，便用话语反驳我，说：“像你这样不称职的发行人员，竟然还敢向我推荐书籍！”通常情况下，遇到这样的情况，...

早些时候，小明总认为最小公倍数这类学问索然无趣，整天埋头于计算哪些数与哪些数的最小公倍数，实在令人头疼，心想掌握这些内容在现实生活中毫无价值。不过，后来发生的一件事却颠覆了他的想法。 某日小明与父亲同乘公交前往少年宫，二人所乘为3路车kaiyun全站登录网页入口，临行之际1路车恰与之同步启动，父亲凝视两车k...

加速度测量设备，亦称速度感应装置，当前在移动设备中普及应用，能够检测仪器在各个方位承受的力度，从而推算出加速度数值kaiyun全站app登录入口，诸如设备中的行进计数功能、晃动识别等众多操作均依赖此类装置完成功能。过去业内普遍认定其与个人隐私关联不大，因此在功能配置方面，手机应用程序可以轻易获取加速度测量数...

根据《2021健康消费洞察报告》的数据，国内大部分家庭的每年健康开销徘徊在500元到5000元之间，公众对于健康方面的投入意愿正逐步增强。现在正值“双十一”购物节，估计很多人已经选购了若干健康相关的商品。 当前，大数据、人工智能等新兴科技日益广泛，智能手环、健身镜、智能体重秤等有助于提升健康的智能设备不断涌现...

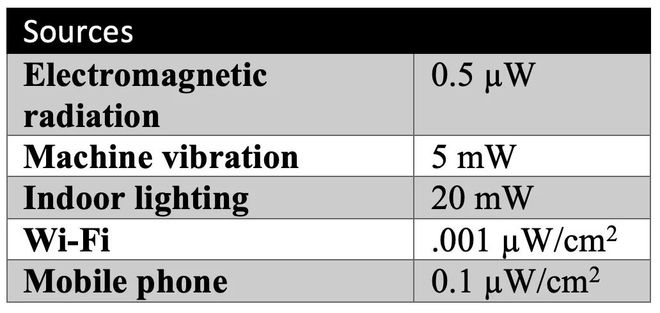
能量采集在物联网方面具备潜力，可以降低甚至无需依赖电池供电。这种优势对那些电池更换困难的设备，包括牲畜监测装置、智慧建筑以及偏远地区的监控设备，显得尤为实用。同时，它也适用于可穿戴电子装置和货物运输追踪等场景。然而，现阶段这项技术尚未得到广泛应用。 这得益于供给端和功率规模有限且时常不稳定。同时，将环境能量转...

锥体上滚实验心得体会 篇一:椎体上滚实验报告 椎体上滚 【实验目的】 使学生加深了解在重力场中物体总是以降低重心,趋 于稳定的运动规律。 动的趋势,同时说明物体势能和动能的相互转换。 【实验仪器】 【实验原理】 能量最低原理指出:物体或系统的能 量总是自然趋向最低状态。本实验中在低端的两根导 轨间距小,锥体停...