林深见鹿（二）：概率论与数理统计（1）

分享兴趣，传播快乐，增长见闻，留下美好！

亲爱的您，这里是LearningYard新学苑。

今天小编为大家带来

“林深见鹿（二）：概率论与数理统计（1）”。

欢迎您的访问！

分享爱好，传递快乐，增长见识，留下美好。

您好，这里是学习园新学院。

今日，编者呈现《深林鹿现（续篇）：概率论与数理统计（其一）》

Welcome to visit!

思维导图

MindMapping

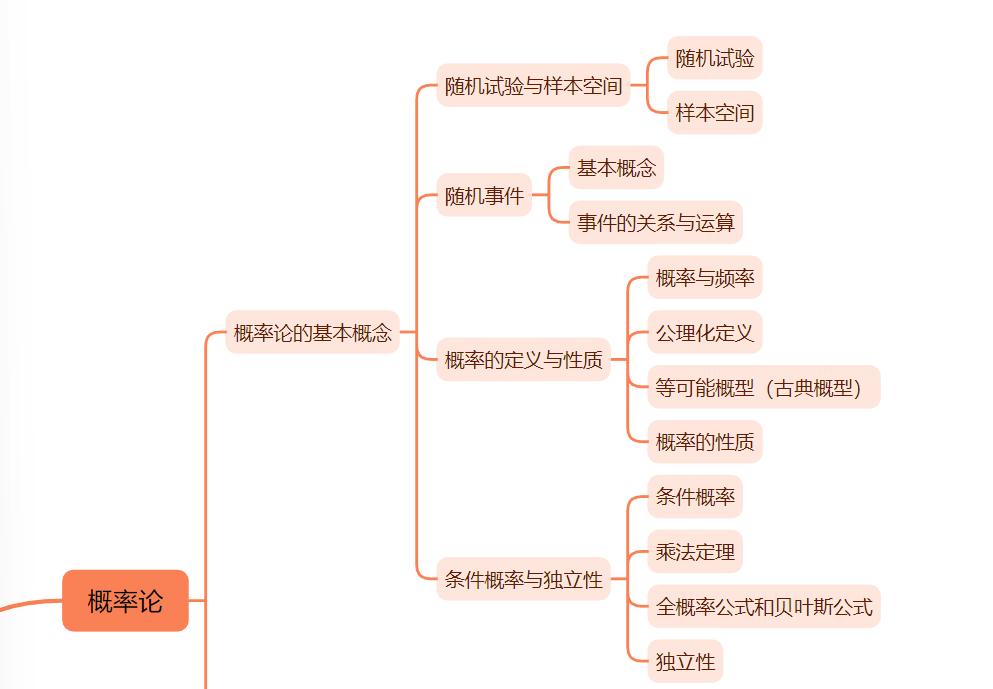
一、理解“随机”

一、Understanding "Randomness"

1. 随机试验——科学描述不确定性

随机现象——以科学方式阐释不确定性

定义：结果不可预知但明确的实验。

一种试验，其结果难以预料却十分明确。

关键点：可重复性 + 结果明确性

要点：可重复性，结果的明确性

例子：抛硬币：结果只能是“正面”或“反面“。

抛掷硬币：其结果仅可能是正面kaiyun.ccm，或者是反面。

2. 样本空间——所有可能结果的集合

样本空间指的是全部潜在结果的集合

说明：试验E全部可能出现的情形集合称作E的样本空间，记作S。这个集合里的每一个情形，也就是试验E的某个结果，叫做样本点。

定义：随机实验E所有可能的结果的全体称作E的样本空间，记作S，样本空间中的任一元素，即E的每一个结果，称为样本点

种类：有穷：投掷骰子时结果集合是{1,2,3,4,5,6}；无穷：考察某个地点每天降水的数值范围。

0,+∞)）。

种类：有限的：掷骰子，S = {1, 2, 3, 4, 5, 6}；无限的：测量某地每日降雨量，S =

0, +∞)).

二、随机事件

二、Random Events

1. 事件本质是样本空间的子集

事件基本上是样本空间中的子集

基本事件：由一个样本点组成的单点集。

基本事件，仅由一个样本点构成的单一集合，没有任何其他元素伴随。

必然事件：S本身，在每次试验中它总是发生的。

这个特定事件就是S，它每次实验时必定会发生。

不可能事件：空集∅，在每次试验中它都不发生。

不可能事件：空集∅，在任何实验中都绝对不会出现。

2. 事件的关系与运算——逻辑的数学表达

事件间的关联与互动——逻辑的数学公式表述

关系（Relationships）：

相等：A发生必导致B发生。

公正性在于，只要A出现，B就必定会出现，这种情况是必然的，没有任何例外。

互斥：A和B不能同时发生。

互斥性：A与B不能同时进行，一个发生则另一个必定不会发生。

对立：A不发生就是Ā发生。

互补性：若A未出现，则Ā会出现。

（对立一定属于互斥）

互补事件必定彼此互斥。

运算（Operations）：

加法交换律：集合A并集集合B等于集合B并集集合A；集合A交集集合B等于集合B交集集合A。

结合律：并集方面，A与B的并集再和C合并开元棋官方正版下载，等于A与B和C合并后的并集；交集方面，A与B的交集再和C合并，等于A与B和C合并后的交集。

结合律（Combination Rule）: 集合A与集合B和集合C的交集，等于集合A与集合B的并集，再与集合A和集合C的并集的交集；集合A与集合B和集合C的并集，等于集合A与集合B的交集kaiyun官方网站登录入口，再与集合A和集合C的交集的并集。

德摩根律（De Morgan's Laws）：

口诀：“交并补差像集合，德摩根律别记错！

记忆法提示：并集与交集的补集性质类似集合；切莫记错德摩根定律！

三、概率的定义

三、Definition of Probability

1. 三种直观定义

三种直观的概率定义

等可能事件类型：计算方法为，目标情形数量除以全部情形数量。

经典概率模型（等概率模型）：公式为概率等于有利结果个数除以所有可能结果总数。

条件：结果有限且等可能。

情况：存在有限且概率相等的可能结果

几何概型：公式：概率=有利区域大小/总区域大小。

几何概率模型：公式为概率等于有利区域的大小除以总区域的大小

例子：在0~1随机取数，≤0.5的概率是50%。

任意取一个介于零和一之间的数值，该数值小于等于零点五的可能性为百分之五十。

频率派主张长期频率的恒定数值，例如硬币抛掷1000次，正面结果大约出现500次。

频率学派方法：长期次数的稳定数值，例如抛掷一枚硬币一千次，大约会得到五百次正面结果。

2.公理化定义——概率的“宪法”

公理化表述，即概率的"基础准则"

三大公理（Three Axioms）：

非负性：对于每一事件B，有P(B|A)≥0。

非负性：对于任意事件B，条件概率P(B|A)都大于等于零。

规范性：对于必然事件S，有P(S|A)=1。

标准化：对于特定事件S，条件概率P在给定A的情况下等于一。

可加性：互斥事件概率可相加。

可加性：互斥事件的概率能够相加合并。

意义：所有概率问题都基于这三条，就像数学中的“游戏规则”。

意义在于，所有概率问题都以这三条公理为根基，如同数学中的游戏规则。

四、条件概率与独立性

四、条件概率与独立关系

1. 条件概率（这是贝叶斯公式的核心应用）

条件机率，是贝叶斯公式的重要实践运用

公式：P(B|A)=P(AB)/P(A)（B已发生）。

条件概率公式是：B在A发生的前提下出现的概率，等于A和B同时出现的概率，除以A出现的概率。

一个人检测为阳性，那么他确实患病的可能性有多大？

一个人检测呈阳性（B），那么他们真的患有疾病（A）的可能性有多大？

2.乘法定理

2. Multiplication Theorem

如果事件A的概率大于零，那么事件AB的概率等于事件A发生条件下事件B的概率乘以事件A的概率

当事件A的概率大于零时，事件AB的概率等于事件B在事件A发生的条件下的概率乘以事件A的概率

3. 全概率与贝叶斯——分解与逆推

全概率法则与贝叶斯定理——拆解与逆向推理

全概率公式表述如下：若事件B₁,B₂等彼此排斥且涵盖所有可能情况，则事件A的概率等于各个条件下事件A概率与对应事件概率的乘积之和。

全概率公式表明：若事件B₁，B₂等彼此互斥且构成完备组，则事件A的概率等于所有条件概率乘以对应事件概率之和，具体为P(A) = P(A|B₁)P(B₁) + P(A|B₂)P(B₂) + 以此类推。

贝叶斯定理表述为：条件概率P(Bⱼ|A)等于后验概率P(A|Bⱼ)乘以先验概率P(Bⱼ)，再除以所有可能原因的总和，即∑P(A|Bᵢ)P(Bᵢ)，这个公式能够实现从结果推导出原因的过程

贝叶斯定理：条件概率Bⱼ在A下的值，等于在Bⱼ下A的条件概率乘以Bⱼ的概率，再除以所有Bᵢ下A的条件概率乘以Bᵢ的概率之和，这个过程用于根据结果推断原因。

4. 独立性——无因果影响

自主权——毫无因果关联

定义：P(AB)=P(A)P(B)。

Definition: P(AB) = P(A)P(B).

错误提醒：单独存在不等于彼此排斥，互斥情形往往彼此依赖，除非其中一项发生的可能性为零。

错误提醒：独立不等于互斥！互斥事件通常不独立，除非其中一个概率为零。

独立性需验证，不能主观假设。

自主性需要经过核实，不能仅凭主观臆断认定。